動脈中的血流動力學參數難以無創測量，基于計算流體力學（CFD）對血流動力學參數進行分析與預測已成為生物力學的重要研究熱點之一。本文通過建立15種合并狹窄和血管瘤病變的理想化左冠狀動脈分叉模型，采用CFD方法對其進行數值仿真，探究了左前降支（LAD）狹窄率和曲率半徑對動脈瘤內血流動力學的影響。本研究對不同狹窄率和曲率半徑下的模型進行比較，觀察發現，隨著狹窄率的增加，振蕩剪切指數（OSI）和相對滯留時間（RRT）呈現增加趨勢；此外，曲率半徑的減小導致血管彎曲程度提高，血管瘤破裂的風險增加。其中，當狹窄率小于60%時，狹窄率對動脈瘤破裂的影響更大；當狹窄率大于60%時，曲率半徑的影響更為顯著。基于本文研究結果可知，綜合考慮狹窄率和曲率半徑對血流動力學參數的影響，可以對動脈瘤的破裂風險進行分析和預測。本文運用CFD方法深入探究了狹窄率和曲率半徑對動脈瘤內血流動力學的影響，為動脈瘤破裂風險的評估提供了新的理論依據和預測手段，具有重要的學術價值和實踐指導意義。
引用本文： 石政加, 桑建兵, 孫麗芳, 李峰韜, 陶雅萍, 楊鵬. 合并血管狹窄左冠狀動脈血管瘤的血流動力學仿真與分析. 生物醫學工程學雜志, 2024, 41(5): 1026-1034. doi: 10.7507/1001-5515.202310038 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
心血管疾病（cardio vascular disease，CVD）的發病率極高，全球范圍內約三分之一的死亡是CVD導致的，例如冠心病、高血壓和心肌梗死等。由于治療成本高，CVD患者需背負沉重的財務負擔。CVD通常發生在冠狀動脈和頸動脈等易感部位，動脈粥樣硬化是CVD發生的主要原因。
冠狀動脈是心臟供血的主要血管之一，血流動力學對冠狀動脈的形態和功能有重要影響。動脈粥樣硬化，即動脈狹窄，是由于動脈壁發生鈣化形成斑塊，導致管腔節段性狹窄。動脈瘤，是指冠狀動脈異常擴張，其直徑超過相鄰正常段的50%[1]，其產生是動脈壁損傷、破壞和變性的結果。動脈狹窄患者的動脈瘤發生率明顯增高，這是由于動脈狹窄發生后，導致動脈內血流發生復雜變化，增加了血管壁的損傷風險。對血流動力學參數進行分析，可幫助人們理解和研究動脈瘤的發生、生長和破裂；而動脈瘤的破裂狀態與較高的振蕩剪切指數（oscillatory shear index，OSI）、相對滯留時間（relative retention time，RRT）和正向壁面剪切應力散度（wall shear stress divergence，WSSD）等因素密切相關[2-5]。
目前，對腦動脈瘤破裂風險的分析已經得到廣泛研究，但是對冠狀動脈瘤（coronary artery aneurysm，CAA）的研究相對較少。有學者研究了動脈瘤的幾何特性對動脈瘤內血流動力學的影響，例如彎曲程度大（甚至扭結）和動脈分叉角的加寬會增加動脈瘤破裂的風險[6-8]。Murayama等[9]分析了各種血流動力學參數的效用，包括OSI及其在動脈瘤破裂風險分析中的作用。文獻[10-12]也肯定了血流動力學參數用于評估動脈瘤破裂風險的有效性。動脈瘤破裂是一種多因素現象，例如精神因素、身體壓力和血壓升高等都可能會引發破裂，而OSI異常閾值的部分代表該區域有繼續擴張和破裂的風險，因此可考慮將OSI異常閾值作為動脈瘤繼續擴張部位或者破裂位置的指標依據。
近年來，很多國內學者也對影響動脈瘤生長和破裂的血流動力學參數進行了研究。Mu等[13]對伴有近端動脈狹窄的個性化顱內動脈瘤模型進行了模擬仿真和試驗驗證，證明了狹窄結構的偏移可以改變射流的方向，從而影響血流沖擊壁面的強度。Mu等[14]對比動脈瘤下游兩個分叉血管間的流量分配變化，結果表明在適當的縱橫比范圍內，顱內動脈瘤的出現可以調節血管狹窄帶來的不良血流變化。王浩然等[15]采用計算流體力學（computational fluid dynamics，CFD）模擬分析左CAA搭橋手術治療的血流動力學參數變化，為臨床手術決策提供血流動力學依據。
研究指出，約三分之一的CAA與阻塞性冠狀動脈疾病相關[16]。Negro等[17]也在臨床表象方面論述了動脈粥樣硬化是CAA最常見的病因。目前已經確定動脈狹窄影響動脈瘤的破裂，即使Fan等[18]對動脈粥樣硬化引起的CAA患者的冠狀動脈進行了形態計量學和血流動力學分析，但有關動脈狹窄影響CAA破裂的研究仍然較少。
當前，對合并動脈狹窄的動脈瘤的破裂風險研究多為個性化研究，即通過重建特定病例的三維模型進行針對性分析，其得出的結論不具有普適性。基于此，本論文通過構建理想化左冠狀動脈分叉模型，充分考慮動脈生理曲率半徑和兩個極限曲率半徑，采用控制變量法對比不同狹窄率模型的仿真結果，探究左前降支（left anterior descending branch，LAD）狹窄率和血管曲率半徑對動脈瘤破裂的影響，并深入理解動脈狹窄和血管曲率半徑對動脈瘤生長和破裂影響的潛在機制，以期實現為臨床提供更加廣泛適用的動脈瘤破裂風險評估方法。
1 合并狹窄的冠狀動脈血管瘤建模
本文在機械設計軟件SolidWorks 2019（Dassault Systemes Inc.，美國）中建立了理想化左主干（left main，LM）、LAD和左回旋支（left circumflex，LCX）分叉血管模型。動脈血管模型的原始數據選取于河北工業大學醫院提供的志愿者CT數據，志愿者為成年無CVD病史的健康女性，26歲。數據采集試驗經河北工業大學倫理審查委員會批準（審批編號：HEBUTaCUC2024051），試驗前受試者閱讀了試驗說明，自愿參加試驗并簽署知情同意書。本研究將LM、LAD和LCX的管腔直徑分別設置為3.8、3.1、2.9 mm，血管壁近似為1 mm，LAD與LM和LCX的分叉角分別近似為180°、70°，將LM、LAD和LCX三條血管都延長30 mm，以便流體能夠在管腔內充分流動，從而減少冠狀動脈曲率半徑導致的速度和壓力分布不均勻。
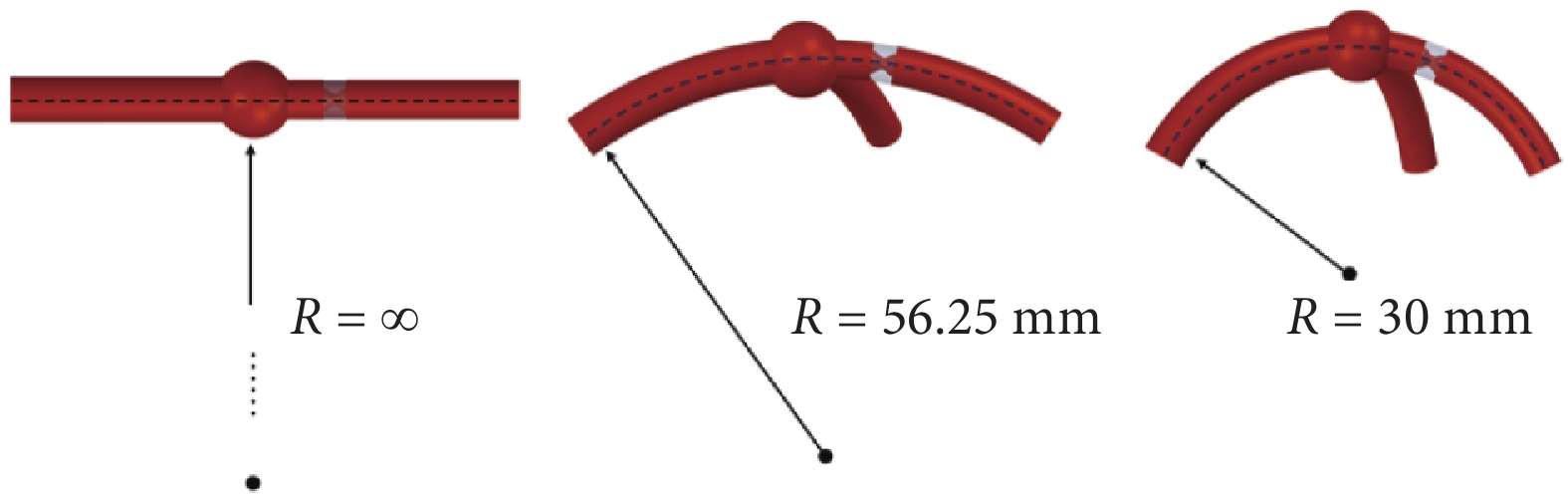
動脈瘤形狀各異，囊狀動脈瘤和梭形動脈瘤是當下研究的主要熱點[19-21]，本文建立了半徑為4 mm的囊狀左CAA三維模型，將心臟視作半徑為R的球體，左冠狀動脈通過血管中心線包覆在心臟表面。根據臨床統計數據，考慮平均生理曲率半徑R = 56.25 mm[22]和兩種極端情況下的曲率半徑R = ∞(無彎曲)和R = 30 mm[23-24]，如圖1所示。
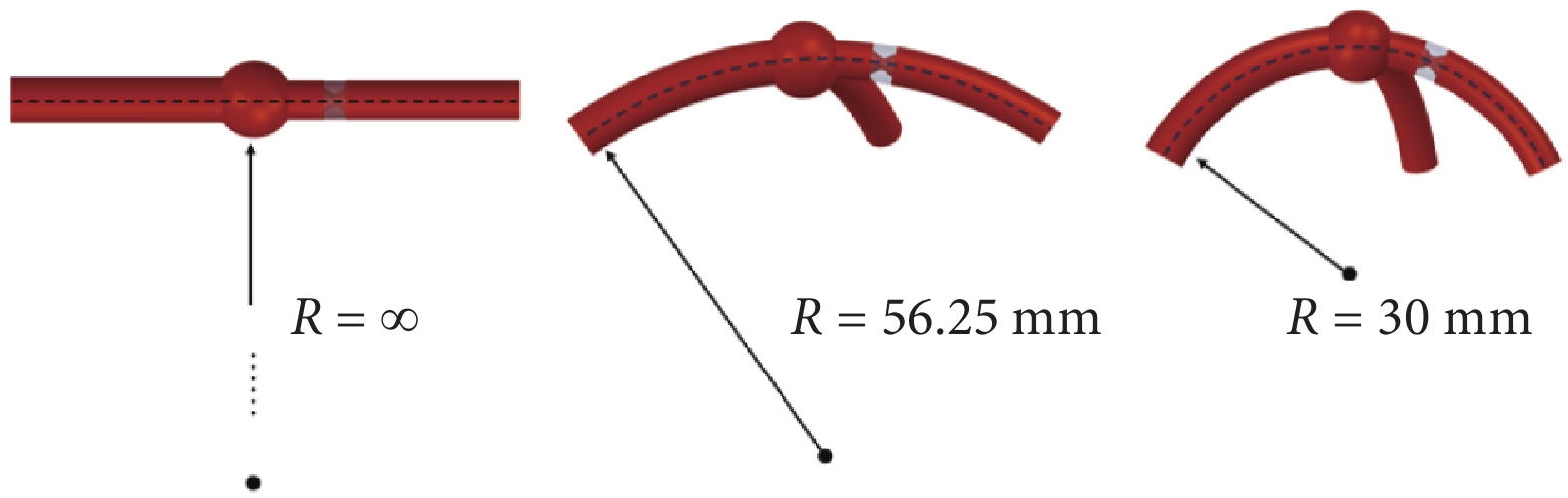圖1
合并狹窄的血管瘤模型曲率半徑
Figure1.
Curvature radius of artery aneurysms with concomitant stenosis
根據臨床數據和調查研究表明，左冠狀分叉動脈中LAD最易產生斑塊[25]，因此在建模時考慮LAD發生狹窄病變，使用余弦斑塊描述狹窄形狀，狹窄模型表達式定義如式(1)所示：
 |
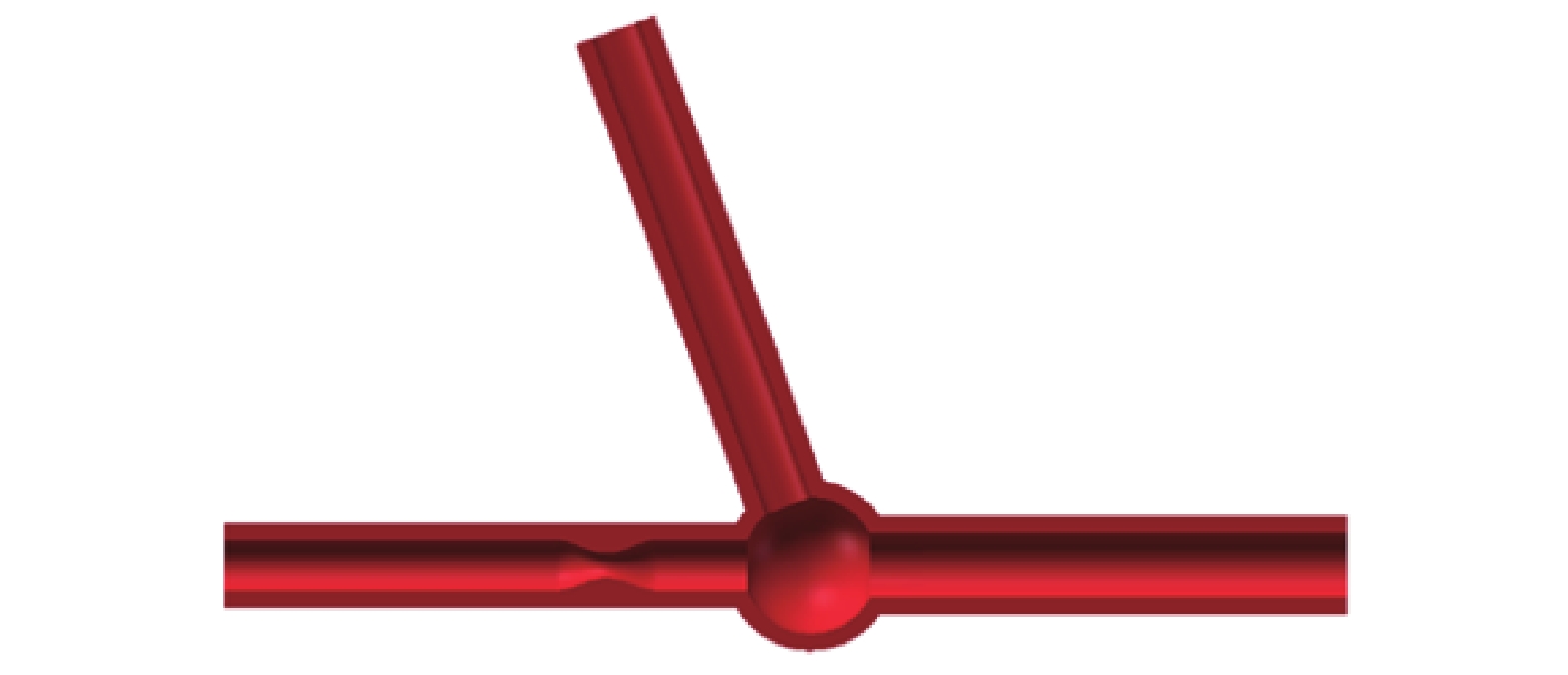
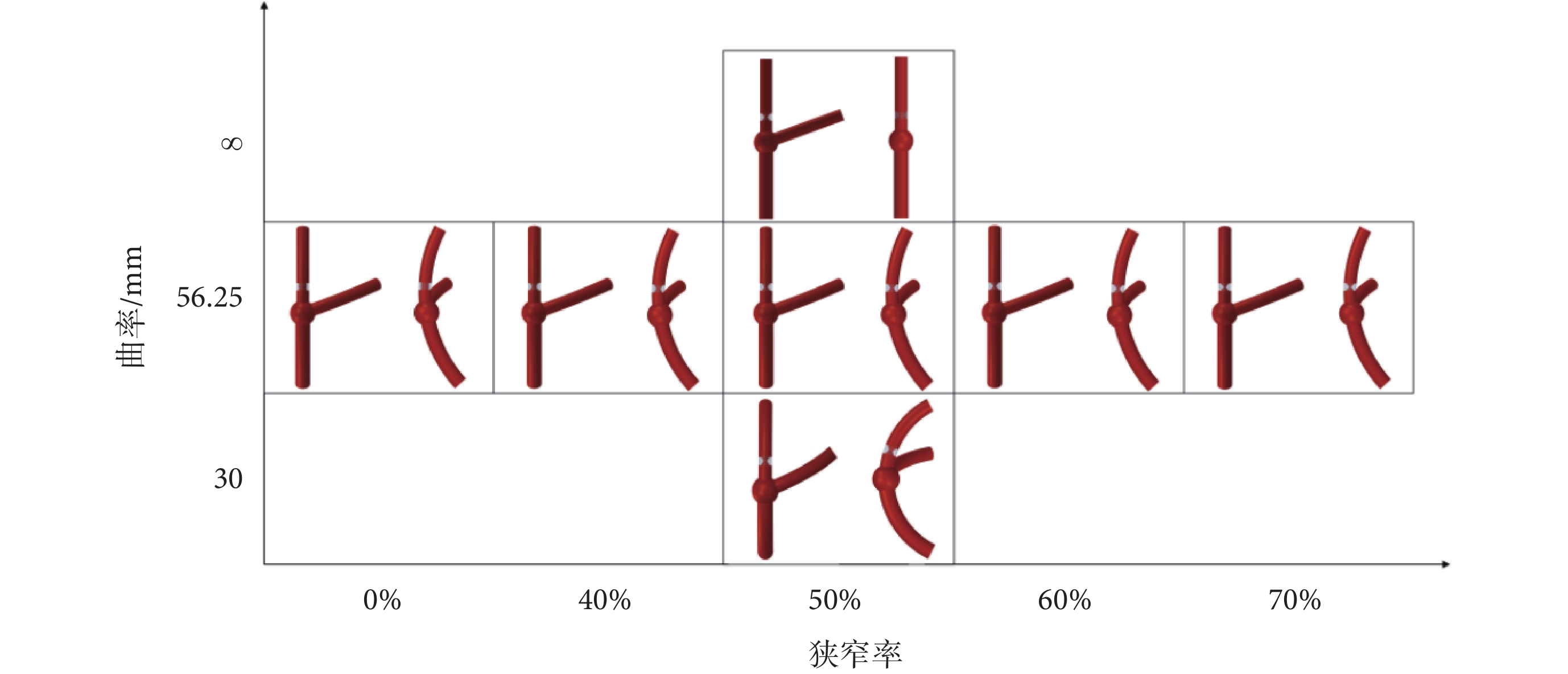
其中，R(x)為狹窄距離中心線的半徑，RC為曲率半徑，RLAD為LAD的內徑，DS為狹窄長度。根據文獻[26]，本文取DS = 4RLAD，SR為狹窄率。分別對SR為0% (無狹窄)、40%、50%、60%和70%的左冠狀動脈進行建模，合并狹窄的血管瘤模型如圖2所示。環形內彈性膜的損傷引起的血管彈性喪失是囊狀顱內動脈瘤形成的重要原因，環形內彈性膜損傷通常發生在動脈分叉點，因此動脈瘤易形成于分叉處。本論文建立的動脈瘤模型位于動脈分叉位置，不同曲率半徑及狹窄率下合并狹窄的動脈瘤模型如圖3所示。
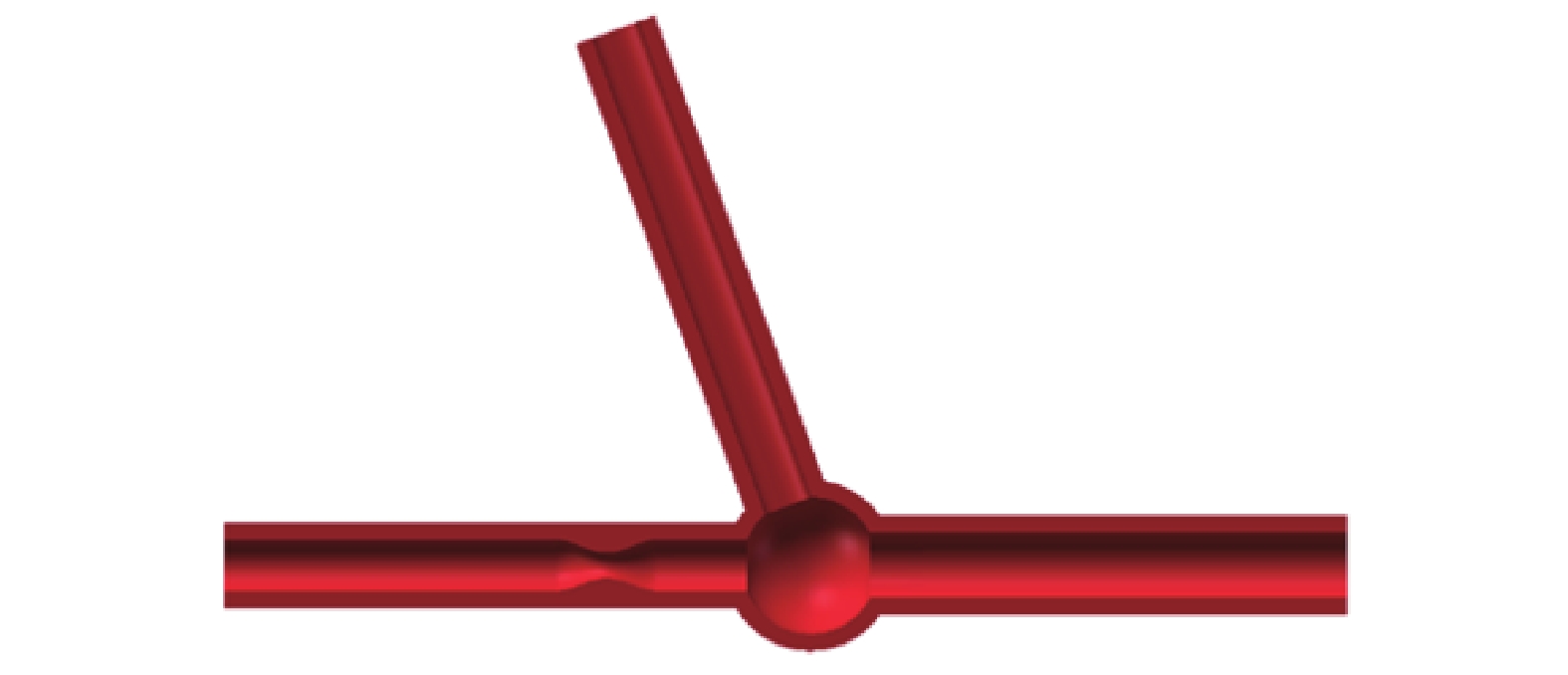圖2
合并狹窄的血管瘤模型
Figure2.
Artery aneurysms with concomitant stenosis
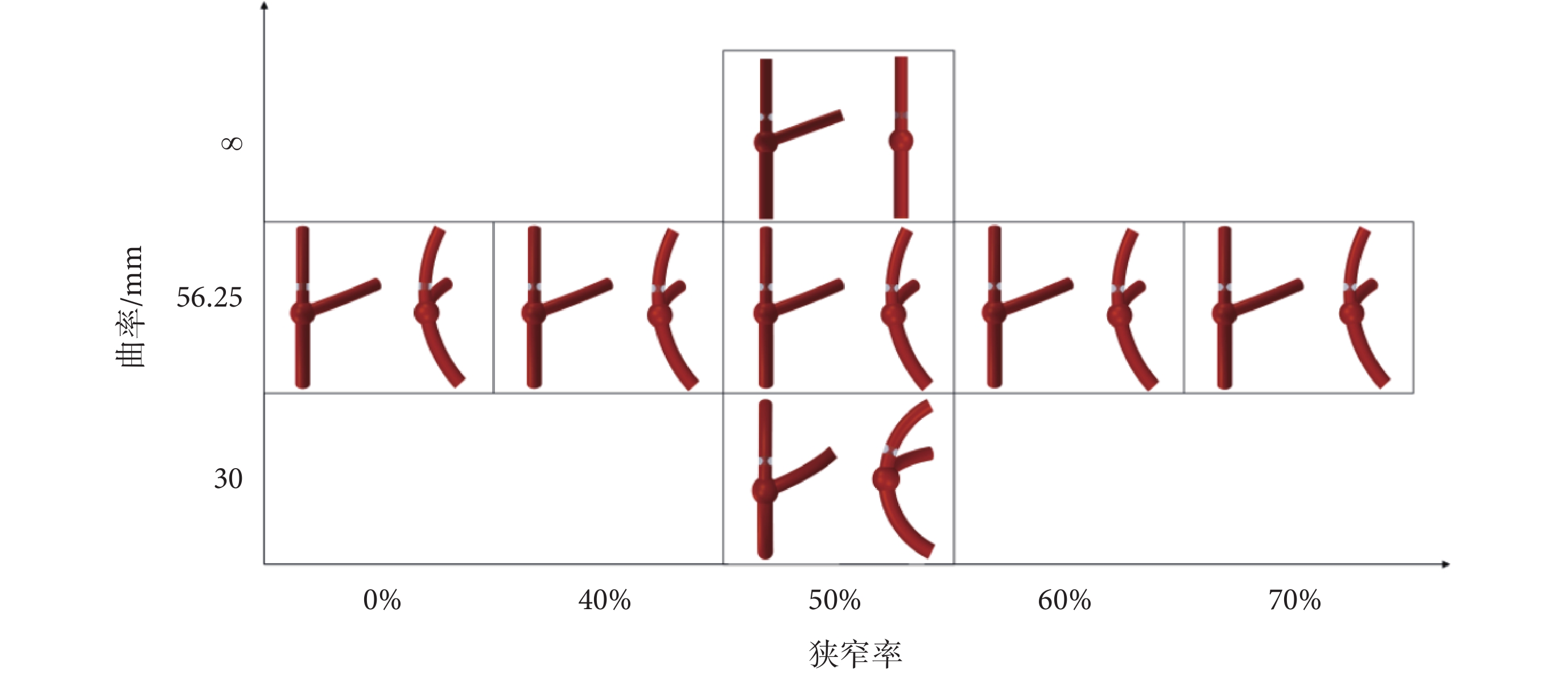圖3
不同曲率半徑及狹窄率下合并狹窄的動脈瘤模型
Figure3.
Artery aneurysms model with concomitant stenosis under different curvature radii and stenosis rates
2 血流動力學仿真與分析
2.1 血流動力學控制方程
基于流體力學基本控制方程，將連續方程、動量方程和能量方程統稱為納維—斯托克斯（Navier-Stokes）方程，簡稱N-S方程，作為描述粘性不可壓縮流體的動量守恒的運動方程，其方程表示如式(2)所示：
 |
其中，ρ表示流體密度，g表示重力加速度，t表示時間，v為速度矢量，p表示流體內部的壓力，μ為血流動力粘性系數。
對比不同的血液粘度模型，研究結果表明，卡洛（Carreau）血液粘度模型通過計算流體力學模擬所產生的動脈中心的時間平均速度與臨床測量值非常吻合[27]，因此本文采用Carreau模型作為血液模型進行數值模擬，其方程表示如式(3)所示：
 |
其中，η為剪切速率為γ時的流體粘度；η∞為高剪切速率下的粘度，取值為0.003 5 Pa
s；η0為低剪切速率下的粘度，取0.056 Pa
s；λ為時間常數，取值為3.131 s；n為冪律指數，在本文中取0.356 8；γ為剪切速率。
2.2 網格劃分及網格無關性分析
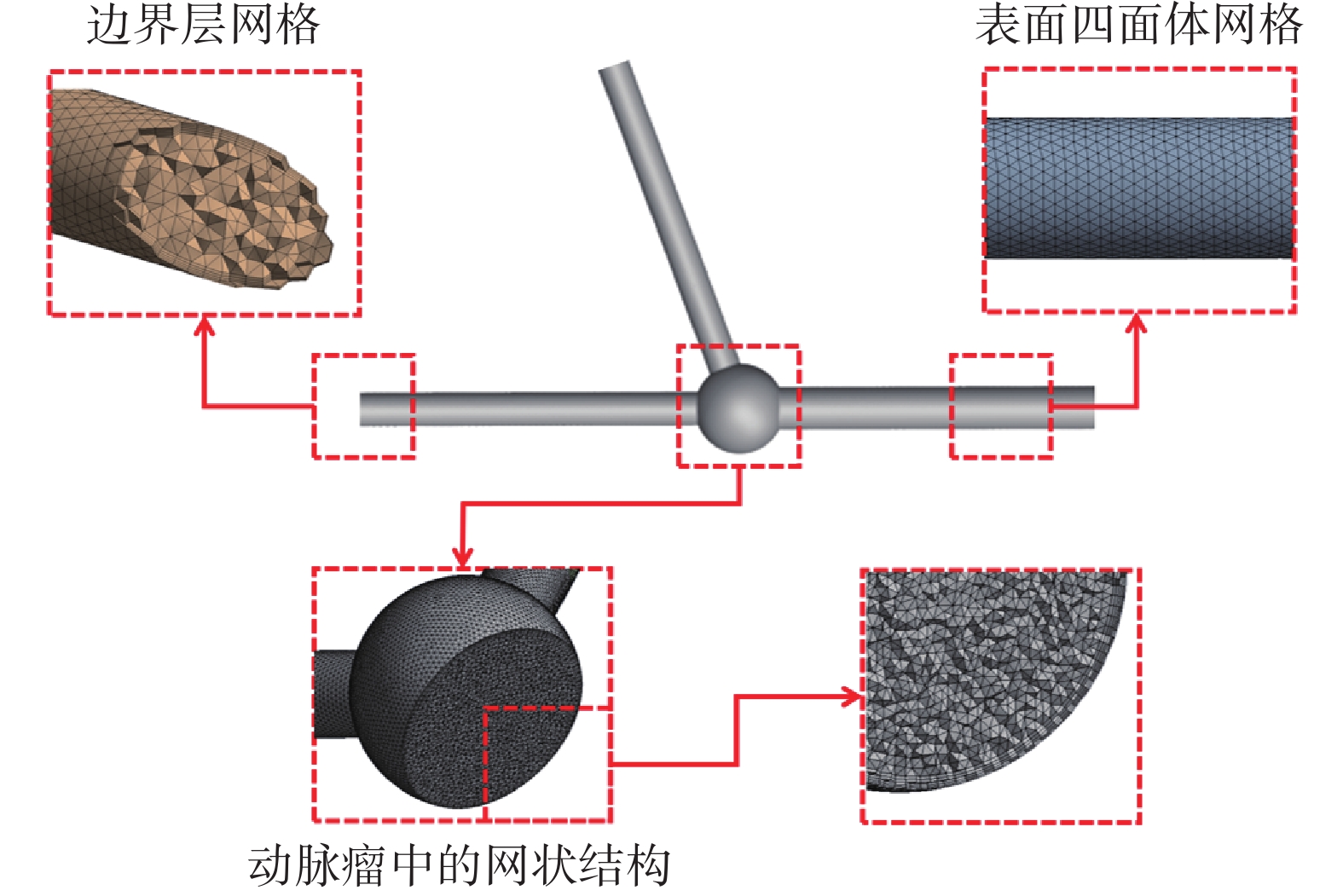
本文采用四面體網格劃分以實現對血管模型內部血流的數值模擬分析，使用無滑移邊界條件，共劃分5層邊界層網格，計算模型各區域的網格結構如圖4所示。
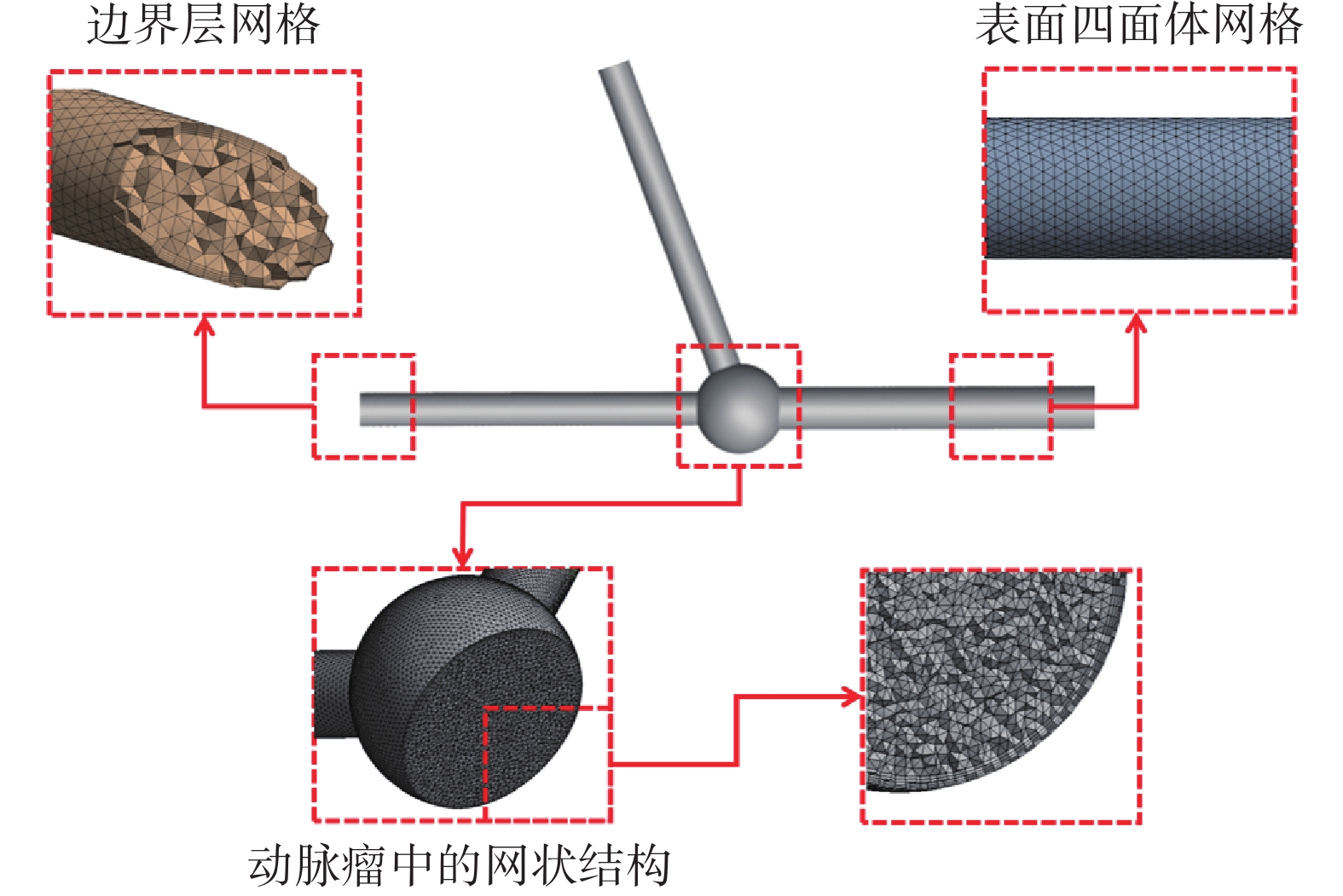圖4
計算模型各區域的網格結構
Figure4.
Calculating the grid structure of each region in the model
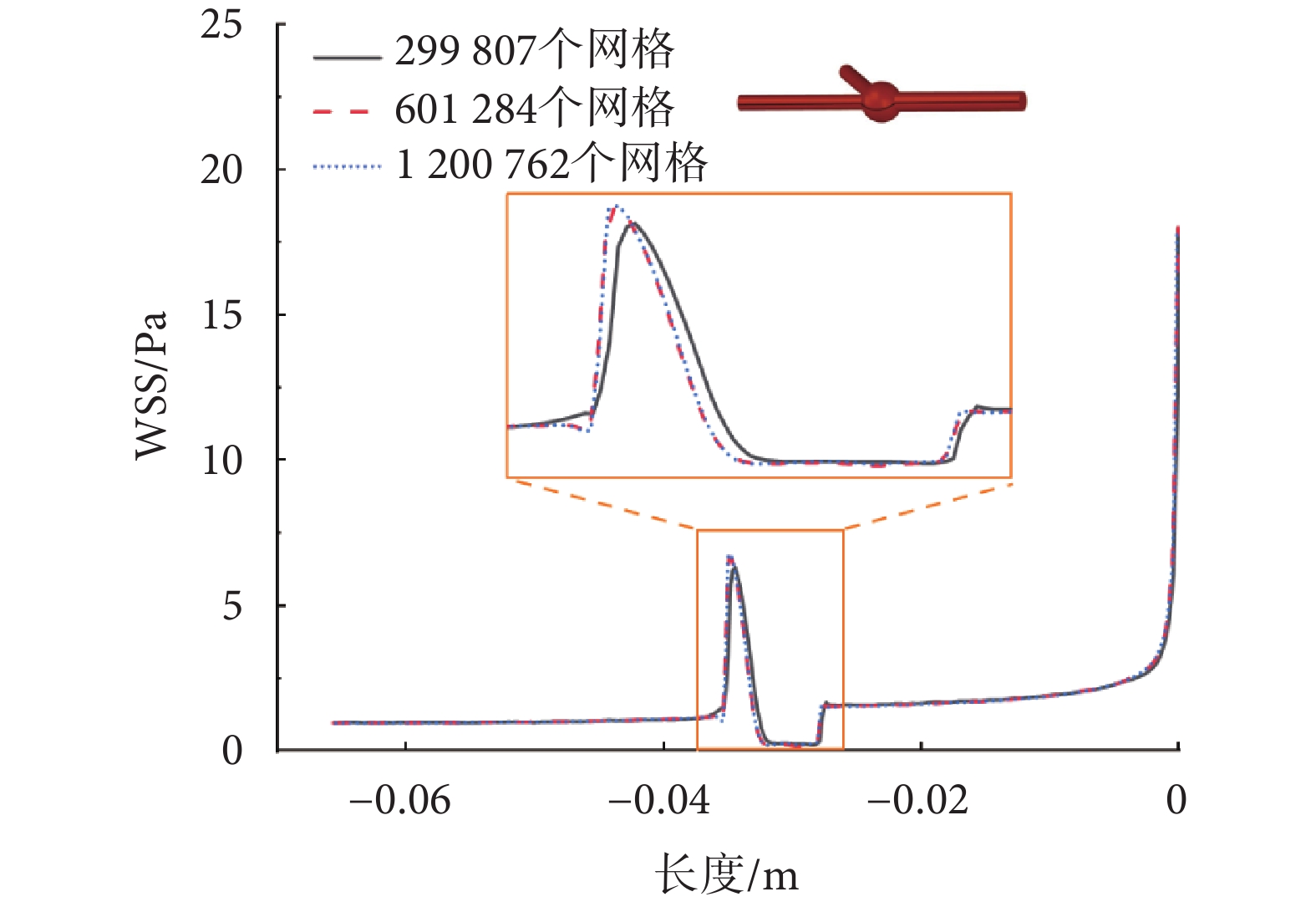
本文以沿血流入口到血流出口的壁面剪切應力（wall shear stress，WSS）為判斷依據，對僅存在血管瘤病變、曲率半徑為∞的左冠狀動脈血管模型進行網格無關性分析；分別設置最小單元尺寸0.34、0.26、0.2 mm，以便于控制網格數量兩倍擴大；并使用0.1 mm網格尺寸對分叉及狹窄區域進行加密。仿真結果如圖5所示，299 807個網格時的壁面剪應力與其他兩種工況相差較大，601 284個網格和1 200 762個網格間WSS相差為1.67%，最終確定601 284個網格時的最小單元尺寸為0.26 mm，并將該尺寸控制參數應用于另外14個模型。
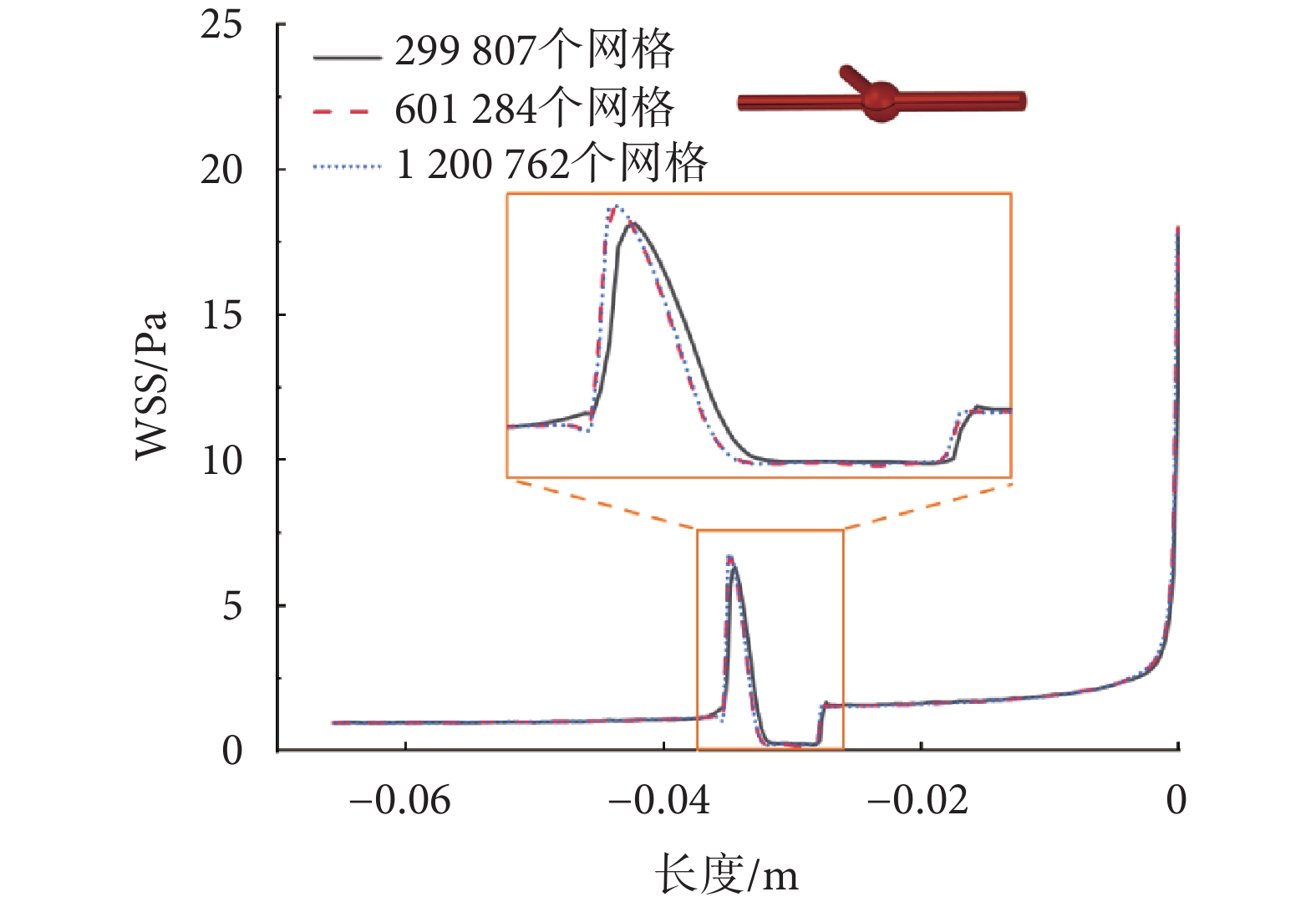圖5
網格無關性分析
Figure5.
Grid independence analysis
2.3 邊界條件選取
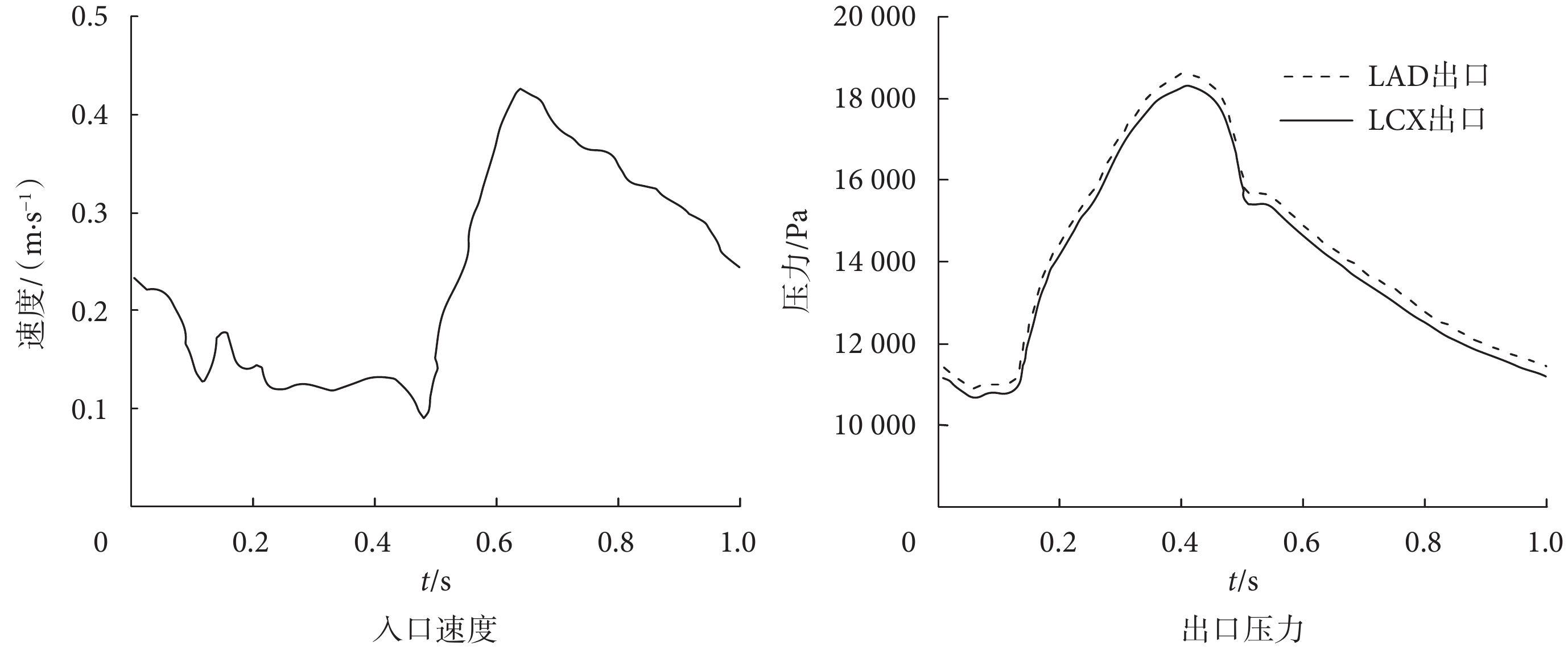
本研究中使用LM的生理測量速度作為入口邊界條件，LAD和LCX處的測量壓力作為出口邊界條件，進行瞬態流動模擬。流體邊界條件如圖6所示，分別為入口速度和出口壓力邊界條件。流體因為具有粘滯性，表現出層流和紊流兩種不同的流動形式。將雷諾數（Reynolds number）以符號Re表示，當Re < 2 300時，流體運動呈層流模式[28]。分別計算得出15種模型的雷諾數，結果表明均為Re < 2 300，因此本文只考慮層流模式。仿真計算過程的時間步長設置為0.01 s。為了消除初始瞬態對計算結果的影響，共模擬3個心動周期，本文對第3個心動周期的仿真結果進行分析。
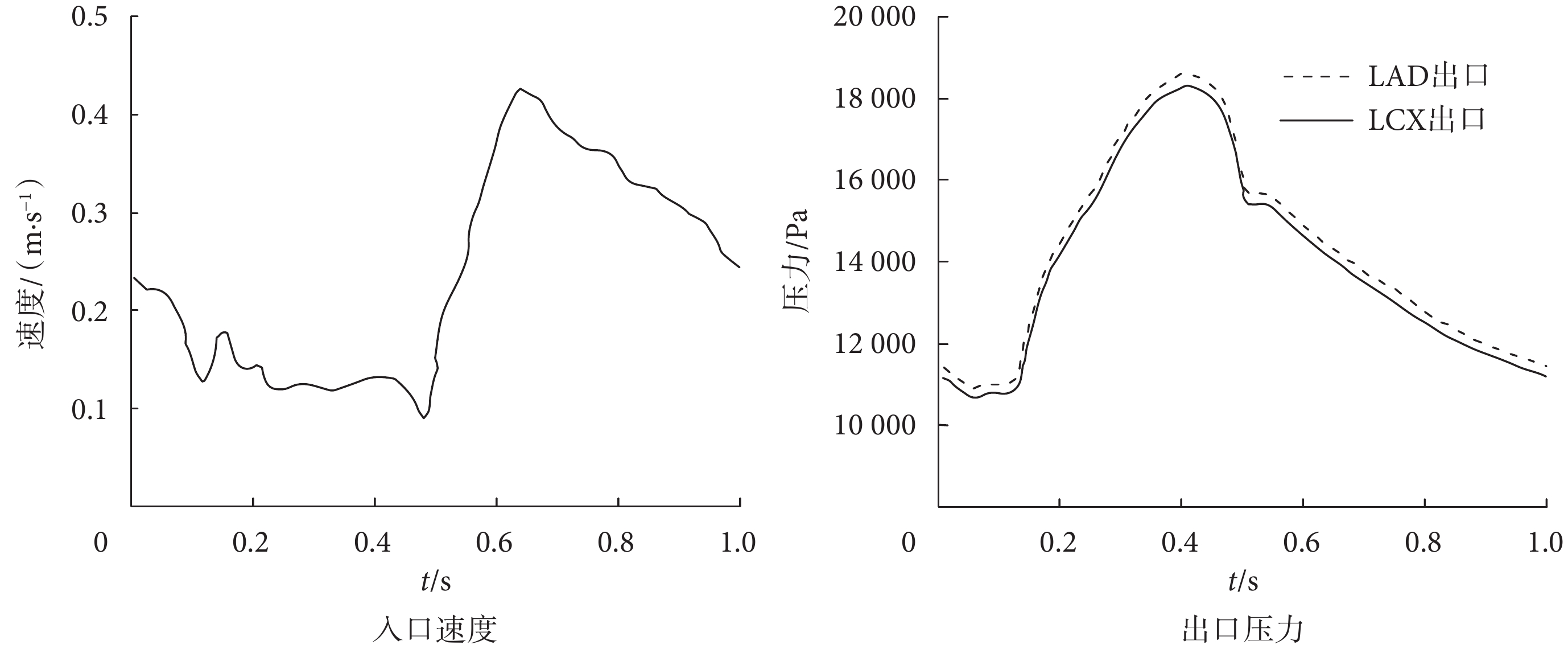圖6
流體邊界條件
Figure6.
Fluid boundary conditions
2.4 血流動力學參數
血流動力學參數已被廣泛應用于評估動脈瘤破裂風險，而OSI能較好地表達動脈中血流的振蕩性質：沒有流動振蕩的區域其OSI的數值為0，完全振蕩的區域其OSI的數值為最大值0.5，過高的OSI值會增加動脈瘤破裂的風險。OSI（以符號OSI表示）的定義如式(4)所示：
 |
其中，τ為瞬時WSS，t為一個心動周期所需的時間，在本文中t = 1 s。
時均WSS（time-averaged WSS, TAWSS）（以符號TAWSS表示）是一種用于描述流場中WSS的參數。它是指在一個周期時間內WSS的平均值，如式(5)所示：
 |
基于TAWSS和OSI計算得出了附加參數RRT（以符號RRT表示），該參數突出顯示了具有高幅度和振蕩WSS的區域，如式(6)所示：
 |
WSSD（以符號WSSD表示），考慮了其梯度和方向，如式(7)所示：
 |
其中，τ為WSS，τi是i方向上WSS的分量，xi是節點橫坐標，如果WSSD的值為正，WSS的作用是拉伸動脈瘤表面；否則，WSS的作用是壓迫動脈瘤表面。WSSD數值的大小表示拉伸或壓縮的強度，因此動脈瘤上顯示正向WSSD的位置更容易破裂。
3 結果分析
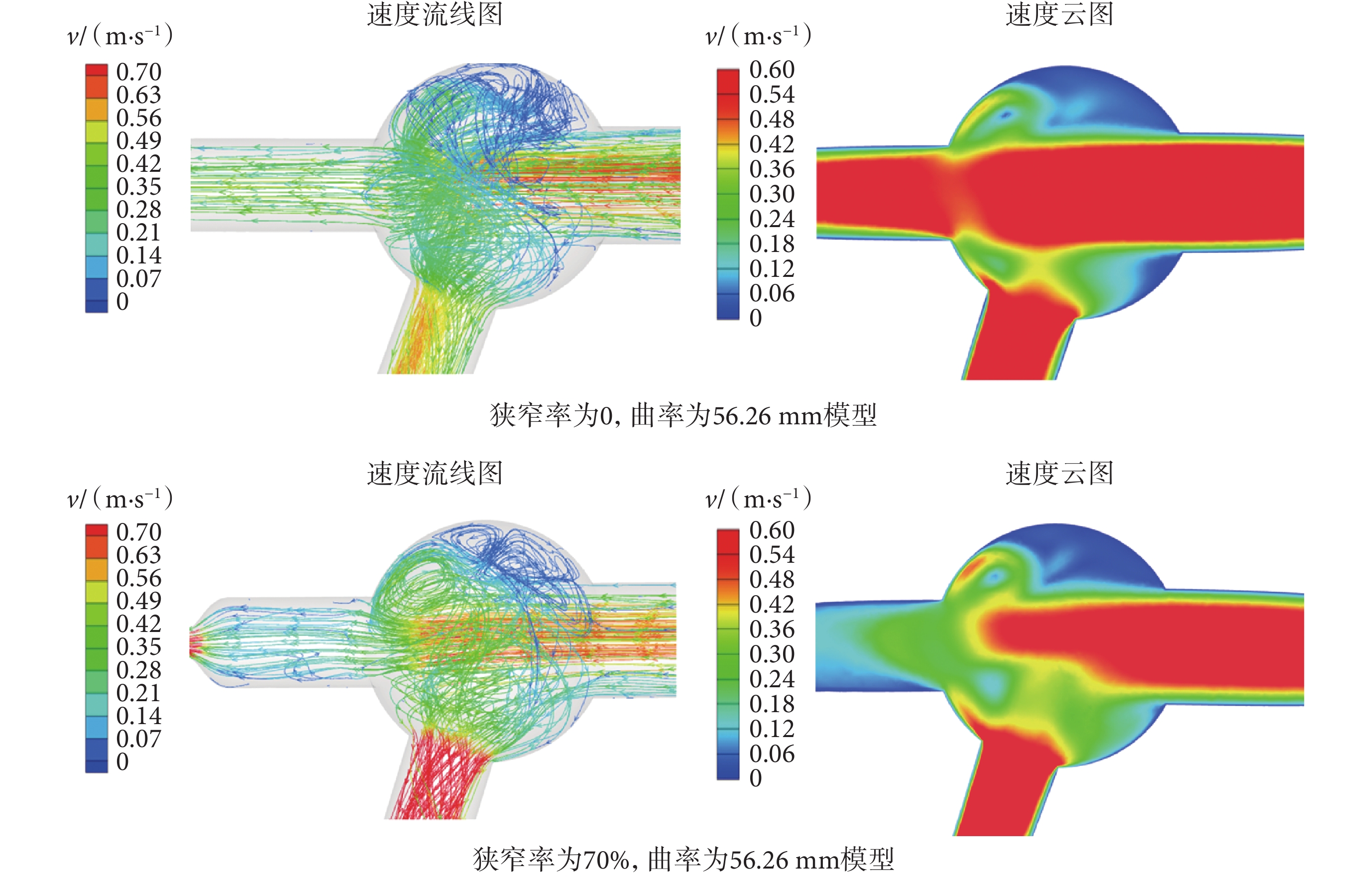
截取流速最高時的動脈瘤橫截面，以便對動脈瘤內的血流進行分析。如圖7所示，分別展示了曲率半徑為56.25 mm情況下無狹窄和狹窄率為70%的速度流線圖及速度云圖。由圖7可知，由于流速的變化和摩擦的作用，血流射入動脈瘤壁面后形成旋轉的渦旋，流體會沿著漩渦方向不斷旋轉，從而形成一個閉合的環流。
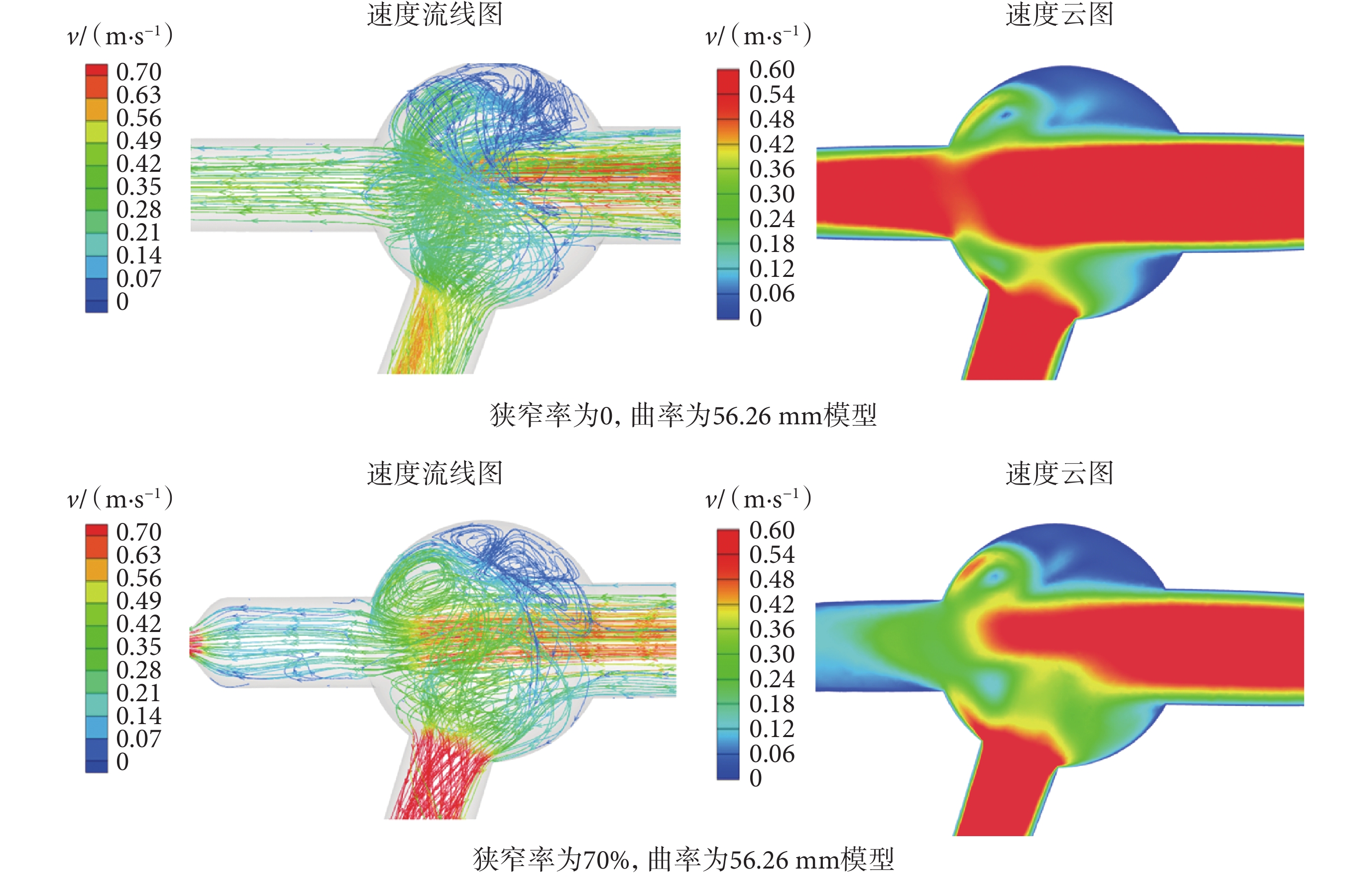圖7
不同狹窄率下的速度流線圖及速度云圖對比
Figure7.
Comparison of velocity streamline maps and velocity cloud maps under different stenosis rates
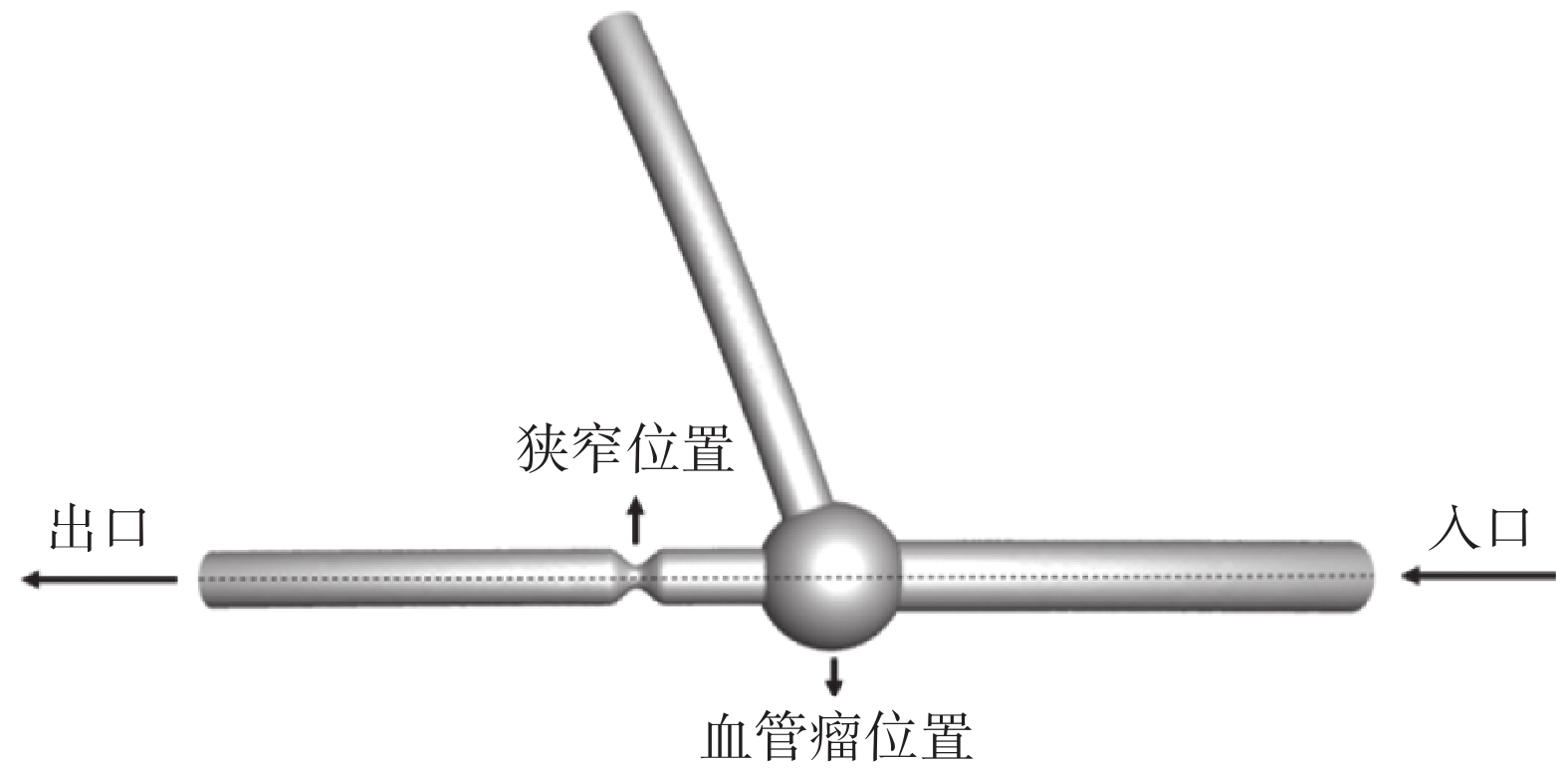
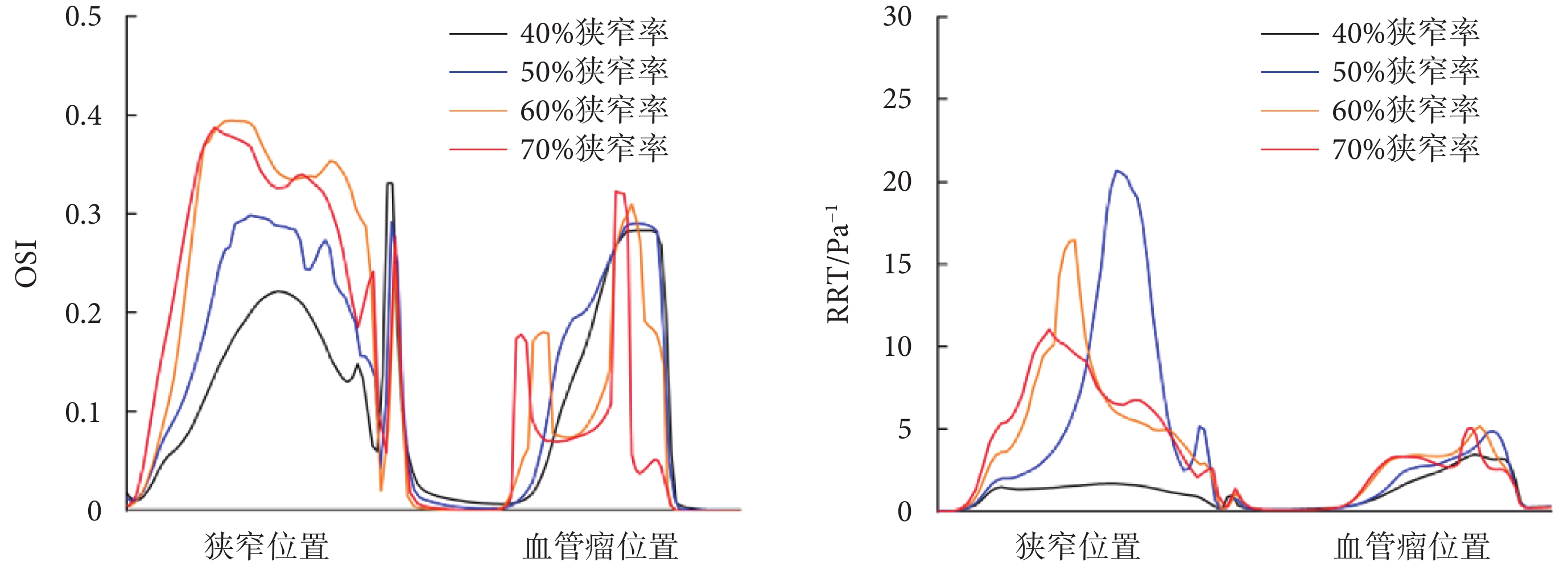
本研究通過有限元分析軟件ANSYS 19.2（ANSYS Inc.，美國）對冠狀動脈流體部分進行仿真計算，得到血管內WSS數值。然后，依次沿血管入口到血管出口采集R=56.25 mm時血管彎曲外側不同狹窄率模型OSI和RRT數值，并對比不同狹窄率下OSI和RRT的分布情況。本文數據采集方式如圖8所示，病變區域的OSI和RRT數據統計結果如圖9所示。
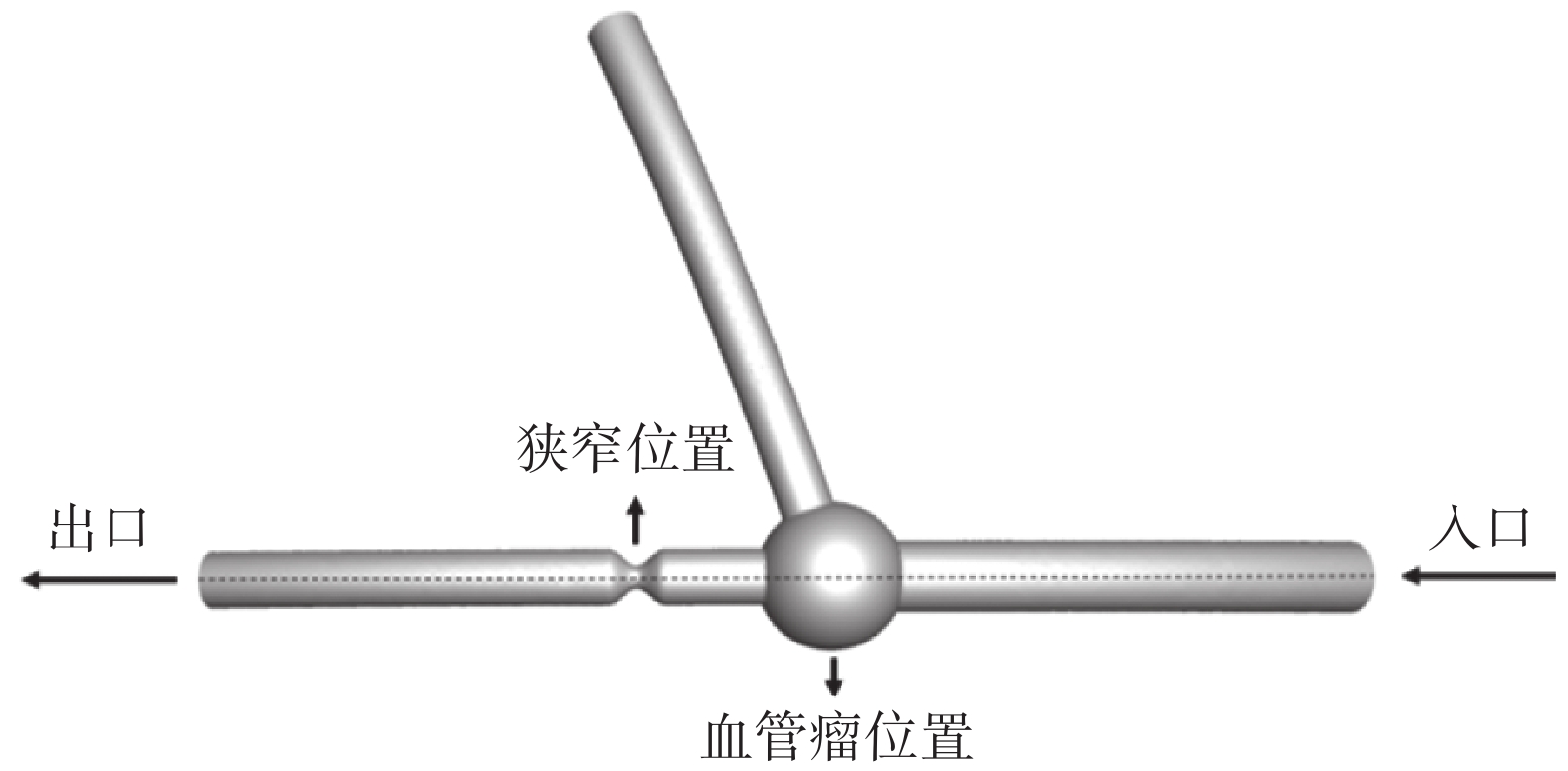圖8
OSI和RRT數據采集
Figure8.
OSI and RRT data collection
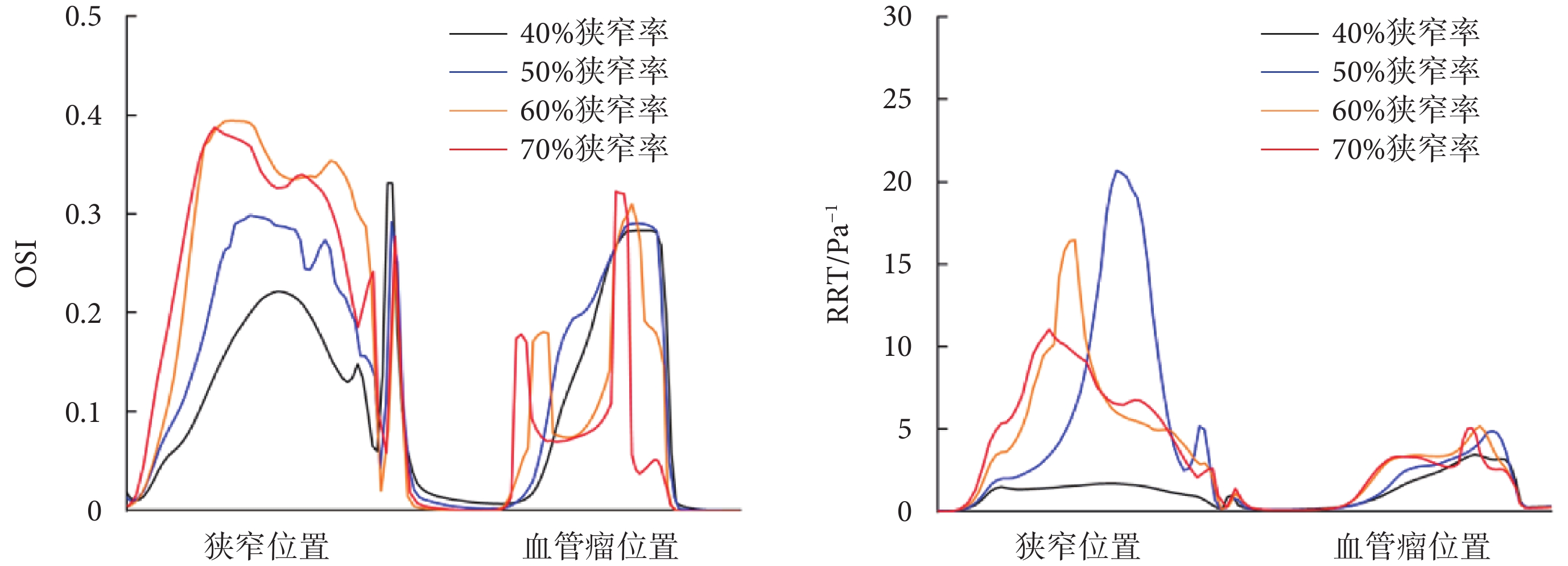圖9
不同狹窄率下OSI、RRT值對比
Figure9.
Comparison of OSI and RRT values under different stenosis rates(Color picture)
由圖9可知，隨著狹窄率的增加，血管瘤位置的OSI和RRT值增大，但是當狹窄率達到70%時，OSI和RRT的極大值與狹窄率為60%模型相比稍有下降，這可能是由于過度狹窄甚至閉塞，反而導致血流速度有所下降，從而在一定程度上減輕了動脈瘤破裂風險。
依據文獻[29]給出動脈瘤的OSI異常閾值（大于0.36），依次對R = ∞、R = 56.25 mm、R = 30 mm無狹窄模型血管彎曲內側的OSI異常結果云圖進行對比，如圖10所示。對比發現，隨著血管彎曲程度增加，彎曲內側血管瘤表面的OSI值變大且OSI異常值面積占比明顯提高，且其他狹窄率模型均符合該規律。
圖10
無狹窄模型彎曲內側血管瘤OSI云圖
Figure10.
OSI cloud map of curved medial hemangioma without stenosis model
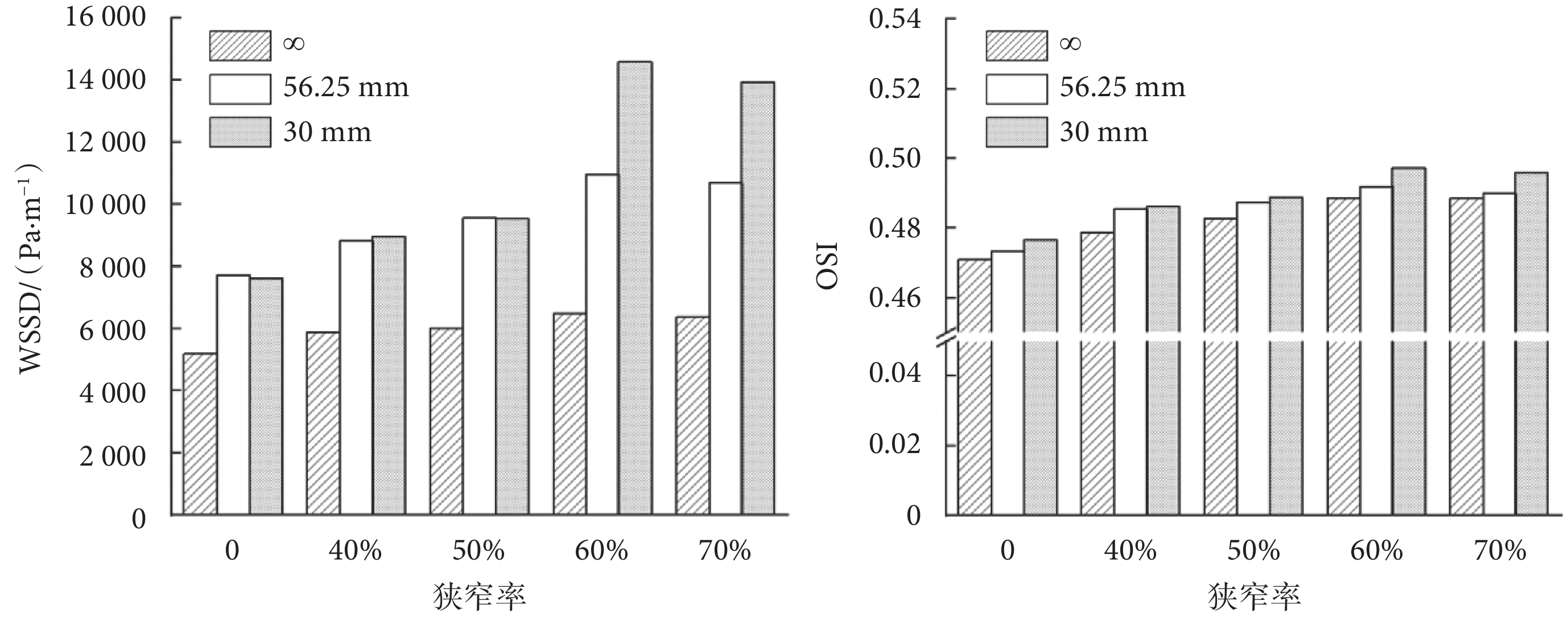
如圖11所示，對比不同曲率半徑下血管瘤表面WSSD和OSI的最大值可以發現，隨著狹窄率和彎曲程度的增加，WSSD和OSI的最大值都呈增加趨勢。當狹窄率為60%和70%時，R = 30 mm時的WSSD和OSI的最大值相較于其他狹窄率模型中R = ∞和R = 56.25 mm時有明顯升高，這表明當血管狹窄達到一定程度時，曲率半徑對血管瘤動力學參數的影響顯著提升。圖11中還可以觀察當狹窄率為70%時，血管瘤的OSI最大值比狹窄率為60%時略低，與圖9中OSI和RRT的變化規律一致。
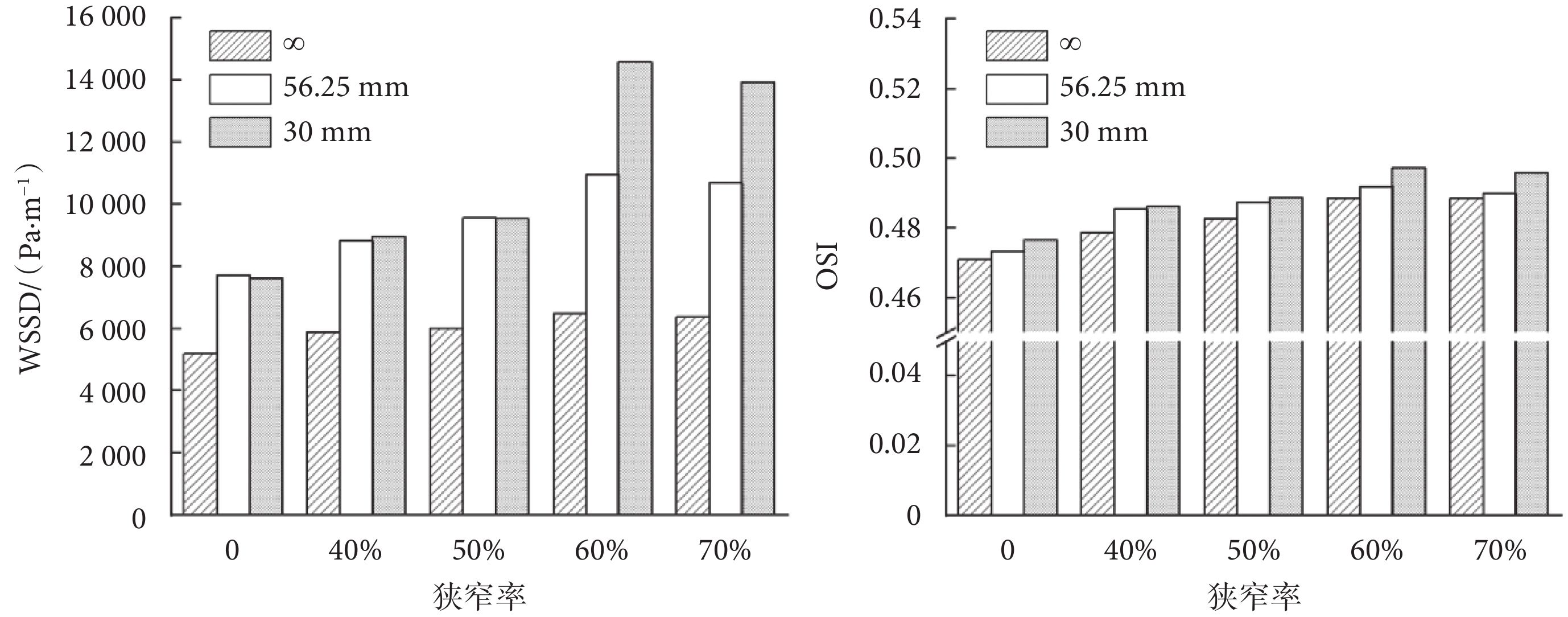圖11
不同狹窄率和曲率半徑下WSSD和OSI最大值對比
Figure11.
Comparison of maximum WSSD and OSI values under different stenosis rates and curvature radii
4 討論
CVD的發生與血流動力學參數的異常直接相關，然而血流動力學參數的體內測量目前仍具有挑戰性，只能通過數值模擬技術對血流動力學參數進行模擬和分析。動脈瘤是一種常見的CVD，動脈瘤破裂會導致嚴重的出血、休克，甚至繼發性器官功能損害。因此，利用血流動力學參數來探究動脈瘤的破裂風險已經成為當前熱門的研究領域。
計算流體力學模擬是血流動力學研究中不可或缺的方法，能夠深入剖析并模擬血液在血管中的流動，以及血流動力學參數的分布情況。這種方法為當下研究提供了一種強有力的工具，能夠用于預測和評估動脈瘤的風險，從而為臨床治療提供更為可靠的科學依據。WSS是計算流體力學分析中最重要的血流動力學參數之一，如果WSS超出正常范圍，可能會導致組織學上的不良病變，從而促使動脈瘤的生長。
當前很多學者通過結合臨床病例，利用WSS分析血管瘤的生長和破裂。Castro等[30]、Cebral等[31]和Hassan等[32]認為高WSS會導致內皮損傷，并引發血管壁重塑和變性過程。相反地，一些研究表明，低WSS區域更容易發生動脈瘤生長和破裂[33-34]。綜上，盡管WSS與動脈瘤的生長和破裂息息相關，其確切作用仍存在爭議，目前尚不清楚是高WSS還是低WSS對動脈瘤產生主要影響。目前的研究通常采取單一的高或低WSS來評估動脈瘤的破裂風險，本文引入WSSD概念，這一參數不僅考慮了WSS的大小，還考慮了其方向性，并據此估算了由WSS凈通量引起的拉伸張力。臨床研究表明，WSSD與動脈瘤表面的薄壁區域之間存在一致性，這為人們理解動脈瘤的生長和破裂提供了新的視角。本文通過綜合考量OSI、RRT和WSSD三個血流動力學參數，對動脈瘤的破裂風險進行評估。這些參數各自為動脈瘤內部血流狀態提供了重要信息，并相互影響，進而影響動脈瘤的穩定性。
研究結果表明，動脈瘤內部的血流常表現為渦流狀態。在動脈瘤的發展階段，通常可以觀察到多個渦流的形成，這導致了動脈壁承受的非均勻壓力增加。與相對穩定的動脈瘤相比，生長過程中的動脈瘤內血流更為復雜，動脈瘤內的多渦流現象和復雜的血流狀態可能導致動脈瘤產生破裂的風險。通過對比狹窄率為70%的模型與無狹窄模型，發現存在狹窄病變的模型中動脈瘤內的血流方向更為復雜，可以觀察到三個方向各異的渦旋結構，進一步增加了動脈瘤破裂的風險。由圖7可知，高血流入射速度下70%狹窄模型中動脈瘤內位于分叉脊對側區域的血流速度極低，幾乎達到停滯狀態，可能導致動脈瘤破裂的風險增加。此外，對比兩模型的速度流線圖顯示，在血流速度最大時，由于狹窄的存在，部分原本流向LAD的血液受到阻礙并回流至動脈瘤內，導致動脈瘤分叉部位的血流速度加快且血流模式變得更加復雜，進一步加劇了動脈瘤的不穩定性。
本研究還深入探討了不同狹窄率和曲率半徑對動脈瘤內血流動力學特性的影響，并據此分析了動脈瘤破裂風險的變化趨勢。研究結果顯示，隨著動脈狹窄率的增加和血管彎曲程度的加劇，動脈瘤的破裂風險呈現出顯著的上升趨勢。然而，當LAD的狹窄率達到或超過60%時，可以觀察到相關的血流動力學參數出現了反常的下降趨勢。這一現象主要歸因于過度狹窄引起血流量減少，血流速度和流量的降低可能會減弱血流對動脈壁的沖擊力和WSS，從而在一定程度上降低了血流的振蕩復雜性和強度。這種變化看似能夠降低動脈瘤的破裂風險，但過度狹窄的同時也可能引發一系列嚴重的病理生理學問題，如血流淤滯和血栓形成等，這些問題同樣會增加動脈瘤破裂的潛在風險。
因此，盡管在某些情況下過度狹窄似乎能夠在一定程度上降低由動脈狹窄和血管彎曲所帶來的動脈瘤破裂風險，但這并不意味著動脈狹窄程度越高，動脈瘤的穩定性就越好。相反，這就需要綜合考慮多個血流動力學參數的變化，例如血流速度、流量和WSS等，以便更全面和準確地評估動脈瘤的破裂風險。
5 結論
本文建立了15個合并狹窄左CAA的三維模型，并利用計算流體動力學方法對模型進行了模擬分析。通過深入探究LAD狹窄程度和血管彎曲程度對血管瘤內血流動力學參數的影響，可以得出以下結論：隨著LAD狹窄率的增加，血管瘤內的OSI、RRT以及WSSD均呈增長趨勢。此外，血管的彎曲形態會導致血管瘤內部血流出現停滯區域，特別在血管彎曲內側，而血管瘤內OSI值顯著升高。并且，OSI風險區域的位置和范圍與血管的彎曲程度緊密相關，而血管的彎曲程度可以通過曲率半徑來量化描述。具體而言，曲率半徑越小，血管彎曲程度越高，將進一步導致動脈瘤內的OSI和WSSD值增大。對比狹窄率和曲率半徑對血流動力學參數的影響可以發現，狹窄率低于50%時，狹窄率對血管瘤血流動力學參數的影響占主要地位；當狹窄率超過50%時，血管彎曲程度對血流動力學參數的影響則變得更為顯著。
本研究通過對血管瘤內的血流動力學參數進行分析，討論了血管瘤的破裂風險及其影響因素，有望為血管瘤破裂風險的臨床評估和治療策略的制定提供重要的理論依據。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：桑建兵和孫麗芳設計了本研究，石政加進行模擬并分析了數據，石政加、李峰韜、陶雅萍和楊鵬討論并共同撰寫了本論文。
倫理聲明：本研究通過了河北工業大學倫理審查委員會的審批（批文編號： HEBUTaCUC2024051）
0 引言
心血管疾病（cardio vascular disease，CVD）的發病率極高，全球范圍內約三分之一的死亡是CVD導致的，例如冠心病、高血壓和心肌梗死等。由于治療成本高，CVD患者需背負沉重的財務負擔。CVD通常發生在冠狀動脈和頸動脈等易感部位，動脈粥樣硬化是CVD發生的主要原因。
冠狀動脈是心臟供血的主要血管之一，血流動力學對冠狀動脈的形態和功能有重要影響。動脈粥樣硬化，即動脈狹窄，是由于動脈壁發生鈣化形成斑塊，導致管腔節段性狹窄。動脈瘤，是指冠狀動脈異常擴張，其直徑超過相鄰正常段的50%[1]，其產生是動脈壁損傷、破壞和變性的結果。動脈狹窄患者的動脈瘤發生率明顯增高，這是由于動脈狹窄發生后，導致動脈內血流發生復雜變化，增加了血管壁的損傷風險。對血流動力學參數進行分析，可幫助人們理解和研究動脈瘤的發生、生長和破裂；而動脈瘤的破裂狀態與較高的振蕩剪切指數（oscillatory shear index，OSI）、相對滯留時間（relative retention time，RRT）和正向壁面剪切應力散度（wall shear stress divergence，WSSD）等因素密切相關[2-5]。
目前，對腦動脈瘤破裂風險的分析已經得到廣泛研究，但是對冠狀動脈瘤（coronary artery aneurysm，CAA）的研究相對較少。有學者研究了動脈瘤的幾何特性對動脈瘤內血流動力學的影響，例如彎曲程度大（甚至扭結）和動脈分叉角的加寬會增加動脈瘤破裂的風險[6-8]。Murayama等[9]分析了各種血流動力學參數的效用，包括OSI及其在動脈瘤破裂風險分析中的作用。文獻[10-12]也肯定了血流動力學參數用于評估動脈瘤破裂風險的有效性。動脈瘤破裂是一種多因素現象，例如精神因素、身體壓力和血壓升高等都可能會引發破裂，而OSI異常閾值的部分代表該區域有繼續擴張和破裂的風險，因此可考慮將OSI異常閾值作為動脈瘤繼續擴張部位或者破裂位置的指標依據。
近年來，很多國內學者也對影響動脈瘤生長和破裂的血流動力學參數進行了研究。Mu等[13]對伴有近端動脈狹窄的個性化顱內動脈瘤模型進行了模擬仿真和試驗驗證，證明了狹窄結構的偏移可以改變射流的方向，從而影響血流沖擊壁面的強度。Mu等[14]對比動脈瘤下游兩個分叉血管間的流量分配變化，結果表明在適當的縱橫比范圍內，顱內動脈瘤的出現可以調節血管狹窄帶來的不良血流變化。王浩然等[15]采用計算流體力學（computational fluid dynamics，CFD）模擬分析左CAA搭橋手術治療的血流動力學參數變化，為臨床手術決策提供血流動力學依據。
研究指出，約三分之一的CAA與阻塞性冠狀動脈疾病相關[16]。Negro等[17]也在臨床表象方面論述了動脈粥樣硬化是CAA最常見的病因。目前已經確定動脈狹窄影響動脈瘤的破裂，即使Fan等[18]對動脈粥樣硬化引起的CAA患者的冠狀動脈進行了形態計量學和血流動力學分析，但有關動脈狹窄影響CAA破裂的研究仍然較少。
當前，對合并動脈狹窄的動脈瘤的破裂風險研究多為個性化研究，即通過重建特定病例的三維模型進行針對性分析，其得出的結論不具有普適性。基于此，本論文通過構建理想化左冠狀動脈分叉模型，充分考慮動脈生理曲率半徑和兩個極限曲率半徑，采用控制變量法對比不同狹窄率模型的仿真結果，探究左前降支（left anterior descending branch，LAD）狹窄率和血管曲率半徑對動脈瘤破裂的影響，并深入理解動脈狹窄和血管曲率半徑對動脈瘤生長和破裂影響的潛在機制，以期實現為臨床提供更加廣泛適用的動脈瘤破裂風險評估方法。
1 合并狹窄的冠狀動脈血管瘤建模
本文在機械設計軟件SolidWorks 2019（Dassault Systemes Inc.，美國）中建立了理想化左主干（left main，LM）、LAD和左回旋支（left circumflex，LCX）分叉血管模型。動脈血管模型的原始數據選取于河北工業大學醫院提供的志愿者CT數據，志愿者為成年無CVD病史的健康女性，26歲。數據采集試驗經河北工業大學倫理審查委員會批準（審批編號：HEBUTaCUC2024051），試驗前受試者閱讀了試驗說明，自愿參加試驗并簽署知情同意書。本研究將LM、LAD和LCX的管腔直徑分別設置為3.8、3.1、2.9 mm，血管壁近似為1 mm，LAD與LM和LCX的分叉角分別近似為180°、70°，將LM、LAD和LCX三條血管都延長30 mm，以便流體能夠在管腔內充分流動，從而減少冠狀動脈曲率半徑導致的速度和壓力分布不均勻。
動脈瘤形狀各異，囊狀動脈瘤和梭形動脈瘤是當下研究的主要熱點[19-21]，本文建立了半徑為4 mm的囊狀左CAA三維模型，將心臟視作半徑為R的球體，左冠狀動脈通過血管中心線包覆在心臟表面。根據臨床統計數據，考慮平均生理曲率半徑R = 56.25 mm[22]和兩種極端情況下的曲率半徑R = ∞(無彎曲)和R = 30 mm[23-24]，如圖1所示。
圖1
合并狹窄的血管瘤模型曲率半徑
Figure1.
Curvature radius of artery aneurysms with concomitant stenosis
根據臨床數據和調查研究表明，左冠狀分叉動脈中LAD最易產生斑塊[25]，因此在建模時考慮LAD發生狹窄病變，使用余弦斑塊描述狹窄形狀，狹窄模型表達式定義如式(1)所示：
|
其中，R(x)為狹窄距離中心線的半徑，RC為曲率半徑，RLAD為LAD的內徑，DS為狹窄長度。根據文獻[26]，本文取DS = 4RLAD，SR為狹窄率。分別對SR為0% (無狹窄)、40%、50%、60%和70%的左冠狀動脈進行建模，合并狹窄的血管瘤模型如圖2所示。環形內彈性膜的損傷引起的血管彈性喪失是囊狀顱內動脈瘤形成的重要原因，環形內彈性膜損傷通常發生在動脈分叉點，因此動脈瘤易形成于分叉處。本論文建立的動脈瘤模型位于動脈分叉位置，不同曲率半徑及狹窄率下合并狹窄的動脈瘤模型如圖3所示。
圖2
合并狹窄的血管瘤模型
Figure2.
Artery aneurysms with concomitant stenosis
圖3
不同曲率半徑及狹窄率下合并狹窄的動脈瘤模型
Figure3.
Artery aneurysms model with concomitant stenosis under different curvature radii and stenosis rates
2 血流動力學仿真與分析
2.1 血流動力學控制方程
基于流體力學基本控制方程，將連續方程、動量方程和能量方程統稱為納維—斯托克斯（Navier-Stokes）方程，簡稱N-S方程，作為描述粘性不可壓縮流體的動量守恒的運動方程，其方程表示如式(2)所示：
|
其中，ρ表示流體密度，g表示重力加速度，t表示時間，v為速度矢量，p表示流體內部的壓力，μ為血流動力粘性系數。
對比不同的血液粘度模型，研究結果表明，卡洛（Carreau）血液粘度模型通過計算流體力學模擬所產生的動脈中心的時間平均速度與臨床測量值非常吻合[27]，因此本文采用Carreau模型作為血液模型進行數值模擬，其方程表示如式(3)所示：
|
其中，η為剪切速率為γ時的流體粘度；η∞為高剪切速率下的粘度，取值為0.003 5 Pas；η0為低剪切速率下的粘度，取0.056 Pas；λ為時間常數，取值為3.131 s；n為冪律指數，在本文中取0.356 8；γ為剪切速率。
2.2 網格劃分及網格無關性分析
本文采用四面體網格劃分以實現對血管模型內部血流的數值模擬分析，使用無滑移邊界條件，共劃分5層邊界層網格，計算模型各區域的網格結構如圖4所示。
圖4
計算模型各區域的網格結構
Figure4.
Calculating the grid structure of each region in the model
本文以沿血流入口到血流出口的壁面剪切應力（wall shear stress，WSS）為判斷依據，對僅存在血管瘤病變、曲率半徑為∞的左冠狀動脈血管模型進行網格無關性分析；分別設置最小單元尺寸0.34、0.26、0.2 mm，以便于控制網格數量兩倍擴大；并使用0.1 mm網格尺寸對分叉及狹窄區域進行加密。仿真結果如圖5所示，299 807個網格時的壁面剪應力與其他兩種工況相差較大，601 284個網格和1 200 762個網格間WSS相差為1.67%，最終確定601 284個網格時的最小單元尺寸為0.26 mm，并將該尺寸控制參數應用于另外14個模型。
圖5
網格無關性分析
Figure5.
Grid independence analysis
2.3 邊界條件選取
本研究中使用LM的生理測量速度作為入口邊界條件，LAD和LCX處的測量壓力作為出口邊界條件，進行瞬態流動模擬。流體邊界條件如圖6所示，分別為入口速度和出口壓力邊界條件。流體因為具有粘滯性，表現出層流和紊流兩種不同的流動形式。將雷諾數（Reynolds number）以符號Re表示，當Re < 2 300時，流體運動呈層流模式[28]。分別計算得出15種模型的雷諾數，結果表明均為Re < 2 300，因此本文只考慮層流模式。仿真計算過程的時間步長設置為0.01 s。為了消除初始瞬態對計算結果的影響，共模擬3個心動周期，本文對第3個心動周期的仿真結果進行分析。
圖6
流體邊界條件
Figure6.
Fluid boundary conditions
2.4 血流動力學參數
血流動力學參數已被廣泛應用于評估動脈瘤破裂風險，而OSI能較好地表達動脈中血流的振蕩性質：沒有流動振蕩的區域其OSI的數值為0，完全振蕩的區域其OSI的數值為最大值0.5，過高的OSI值會增加動脈瘤破裂的風險。OSI（以符號OSI表示）的定義如式(4)所示：
|
其中，τ為瞬時WSS，t為一個心動周期所需的時間，在本文中t = 1 s。
時均WSS（time-averaged WSS, TAWSS）（以符號TAWSS表示）是一種用于描述流場中WSS的參數。它是指在一個周期時間內WSS的平均值，如式(5)所示：
|
基于TAWSS和OSI計算得出了附加參數RRT（以符號RRT表示），該參數突出顯示了具有高幅度和振蕩WSS的區域，如式(6)所示：
|
WSSD（以符號WSSD表示），考慮了其梯度和方向，如式(7)所示：
|
其中，τ為WSS，τi是i方向上WSS的分量，xi是節點橫坐標，如果WSSD的值為正，WSS的作用是拉伸動脈瘤表面；否則，WSS的作用是壓迫動脈瘤表面。WSSD數值的大小表示拉伸或壓縮的強度，因此動脈瘤上顯示正向WSSD的位置更容易破裂。
3 結果分析
截取流速最高時的動脈瘤橫截面，以便對動脈瘤內的血流進行分析。如圖7所示，分別展示了曲率半徑為56.25 mm情況下無狹窄和狹窄率為70%的速度流線圖及速度云圖。由圖7可知，由于流速的變化和摩擦的作用，血流射入動脈瘤壁面后形成旋轉的渦旋，流體會沿著漩渦方向不斷旋轉，從而形成一個閉合的環流。
圖7
不同狹窄率下的速度流線圖及速度云圖對比
Figure7.
Comparison of velocity streamline maps and velocity cloud maps under different stenosis rates
本研究通過有限元分析軟件ANSYS 19.2（ANSYS Inc.，美國）對冠狀動脈流體部分進行仿真計算，得到血管內WSS數值。然后，依次沿血管入口到血管出口采集R=56.25 mm時血管彎曲外側不同狹窄率模型OSI和RRT數值，并對比不同狹窄率下OSI和RRT的分布情況。本文數據采集方式如圖8所示，病變區域的OSI和RRT數據統計結果如圖9所示。
圖8
OSI和RRT數據采集
Figure8.
OSI and RRT data collection
圖9
不同狹窄率下OSI、RRT值對比
Figure9.
Comparison of OSI and RRT values under different stenosis rates(Color picture)
由圖9可知，隨著狹窄率的增加，血管瘤位置的OSI和RRT值增大，但是當狹窄率達到70%時，OSI和RRT的極大值與狹窄率為60%模型相比稍有下降，這可能是由于過度狹窄甚至閉塞，反而導致血流速度有所下降，從而在一定程度上減輕了動脈瘤破裂風險。
依據文獻[29]給出動脈瘤的OSI異常閾值（大于0.36），依次對R = ∞、R = 56.25 mm、R = 30 mm無狹窄模型血管彎曲內側的OSI異常結果云圖進行對比，如圖10所示。對比發現，隨著血管彎曲程度增加，彎曲內側血管瘤表面的OSI值變大且OSI異常值面積占比明顯提高，且其他狹窄率模型均符合該規律。
圖10
無狹窄模型彎曲內側血管瘤OSI云圖
Figure10.
OSI cloud map of curved medial hemangioma without stenosis model
如圖11所示，對比不同曲率半徑下血管瘤表面WSSD和OSI的最大值可以發現，隨著狹窄率和彎曲程度的增加，WSSD和OSI的最大值都呈增加趨勢。當狹窄率為60%和70%時，R = 30 mm時的WSSD和OSI的最大值相較于其他狹窄率模型中R = ∞和R = 56.25 mm時有明顯升高，這表明當血管狹窄達到一定程度時，曲率半徑對血管瘤動力學參數的影響顯著提升。圖11中還可以觀察當狹窄率為70%時，血管瘤的OSI最大值比狹窄率為60%時略低，與圖9中OSI和RRT的變化規律一致。
圖11
不同狹窄率和曲率半徑下WSSD和OSI最大值對比
Figure11.
Comparison of maximum WSSD and OSI values under different stenosis rates and curvature radii
4 討論
CVD的發生與血流動力學參數的異常直接相關，然而血流動力學參數的體內測量目前仍具有挑戰性，只能通過數值模擬技術對血流動力學參數進行模擬和分析。動脈瘤是一種常見的CVD，動脈瘤破裂會導致嚴重的出血、休克，甚至繼發性器官功能損害。因此，利用血流動力學參數來探究動脈瘤的破裂風險已經成為當前熱門的研究領域。
計算流體力學模擬是血流動力學研究中不可或缺的方法，能夠深入剖析并模擬血液在血管中的流動，以及血流動力學參數的分布情況。這種方法為當下研究提供了一種強有力的工具，能夠用于預測和評估動脈瘤的風險，從而為臨床治療提供更為可靠的科學依據。WSS是計算流體力學分析中最重要的血流動力學參數之一，如果WSS超出正常范圍，可能會導致組織學上的不良病變，從而促使動脈瘤的生長。
當前很多學者通過結合臨床病例，利用WSS分析血管瘤的生長和破裂。Castro等[30]、Cebral等[31]和Hassan等[32]認為高WSS會導致內皮損傷，并引發血管壁重塑和變性過程。相反地，一些研究表明，低WSS區域更容易發生動脈瘤生長和破裂[33-34]。綜上，盡管WSS與動脈瘤的生長和破裂息息相關，其確切作用仍存在爭議，目前尚不清楚是高WSS還是低WSS對動脈瘤產生主要影響。目前的研究通常采取單一的高或低WSS來評估動脈瘤的破裂風險，本文引入WSSD概念，這一參數不僅考慮了WSS的大小，還考慮了其方向性，并據此估算了由WSS凈通量引起的拉伸張力。臨床研究表明，WSSD與動脈瘤表面的薄壁區域之間存在一致性，這為人們理解動脈瘤的生長和破裂提供了新的視角。本文通過綜合考量OSI、RRT和WSSD三個血流動力學參數，對動脈瘤的破裂風險進行評估。這些參數各自為動脈瘤內部血流狀態提供了重要信息，并相互影響，進而影響動脈瘤的穩定性。
研究結果表明，動脈瘤內部的血流常表現為渦流狀態。在動脈瘤的發展階段，通常可以觀察到多個渦流的形成，這導致了動脈壁承受的非均勻壓力增加。與相對穩定的動脈瘤相比，生長過程中的動脈瘤內血流更為復雜，動脈瘤內的多渦流現象和復雜的血流狀態可能導致動脈瘤產生破裂的風險。通過對比狹窄率為70%的模型與無狹窄模型，發現存在狹窄病變的模型中動脈瘤內的血流方向更為復雜，可以觀察到三個方向各異的渦旋結構，進一步增加了動脈瘤破裂的風險。由圖7可知，高血流入射速度下70%狹窄模型中動脈瘤內位于分叉脊對側區域的血流速度極低，幾乎達到停滯狀態，可能導致動脈瘤破裂的風險增加。此外，對比兩模型的速度流線圖顯示，在血流速度最大時，由于狹窄的存在，部分原本流向LAD的血液受到阻礙并回流至動脈瘤內，導致動脈瘤分叉部位的血流速度加快且血流模式變得更加復雜，進一步加劇了動脈瘤的不穩定性。
本研究還深入探討了不同狹窄率和曲率半徑對動脈瘤內血流動力學特性的影響，并據此分析了動脈瘤破裂風險的變化趨勢。研究結果顯示，隨著動脈狹窄率的增加和血管彎曲程度的加劇，動脈瘤的破裂風險呈現出顯著的上升趨勢。然而，當LAD的狹窄率達到或超過60%時，可以觀察到相關的血流動力學參數出現了反常的下降趨勢。這一現象主要歸因于過度狹窄引起血流量減少，血流速度和流量的降低可能會減弱血流對動脈壁的沖擊力和WSS，從而在一定程度上降低了血流的振蕩復雜性和強度。這種變化看似能夠降低動脈瘤的破裂風險，但過度狹窄的同時也可能引發一系列嚴重的病理生理學問題，如血流淤滯和血栓形成等，這些問題同樣會增加動脈瘤破裂的潛在風險。
因此，盡管在某些情況下過度狹窄似乎能夠在一定程度上降低由動脈狹窄和血管彎曲所帶來的動脈瘤破裂風險，但這并不意味著動脈狹窄程度越高，動脈瘤的穩定性就越好。相反，這就需要綜合考慮多個血流動力學參數的變化，例如血流速度、流量和WSS等，以便更全面和準確地評估動脈瘤的破裂風險。
5 結論
本文建立了15個合并狹窄左CAA的三維模型，并利用計算流體動力學方法對模型進行了模擬分析。通過深入探究LAD狹窄程度和血管彎曲程度對血管瘤內血流動力學參數的影響，可以得出以下結論：隨著LAD狹窄率的增加，血管瘤內的OSI、RRT以及WSSD均呈增長趨勢。此外，血管的彎曲形態會導致血管瘤內部血流出現停滯區域，特別在血管彎曲內側，而血管瘤內OSI值顯著升高。并且，OSI風險區域的位置和范圍與血管的彎曲程度緊密相關，而血管的彎曲程度可以通過曲率半徑來量化描述。具體而言，曲率半徑越小，血管彎曲程度越高，將進一步導致動脈瘤內的OSI和WSSD值增大。對比狹窄率和曲率半徑對血流動力學參數的影響可以發現，狹窄率低于50%時，狹窄率對血管瘤血流動力學參數的影響占主要地位；當狹窄率超過50%時，血管彎曲程度對血流動力學參數的影響則變得更為顯著。
本研究通過對血管瘤內的血流動力學參數進行分析，討論了血管瘤的破裂風險及其影響因素，有望為血管瘤破裂風險的臨床評估和治療策略的制定提供重要的理論依據。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：桑建兵和孫麗芳設計了本研究，石政加進行模擬并分析了數據，石政加、李峰韜、陶雅萍和楊鵬討論并共同撰寫了本論文。
倫理聲明：本研究通過了河北工業大學倫理審查委員會的審批（批文編號： HEBUTaCUC2024051）
