為了研究直接心室輔助的生物力學影響以及探究最優的加載模式，本文基于有限元方法建立了心衰患者的左心室模型，并提出了一種維持壓迫力峰值的加載模式，從血流動力學和生物力學兩個方面與傳統的正弦加載模式進行了對比。結果表明，兩種模式都能顯著提升血流動力學參數，射血分數分別從基線29.33%增加到37.32%與37.77%，峰值壓力、每搏量和每搏功等參數都有所增加；且兩種模式的應力集中、過度纖維應變等現象均有所改善。然而，當考慮到輔助裝置工作周期的相位誤差時，本文所提出的輔助模式受到的影響更小，故本文研究或可為直接心室輔助裝置的設計和優化提供理論支持。
引用本文： 李宸, 強賢杰, 張盛, 王天博, 劉曉翰, 張悅, 黃剛, 張小剛, 徐俊波, 靳忠民. 基于有限元方法的直接心室輔助加載模式研究. 生物醫學工程學雜志, 2024, 41(4): 782-789. doi: 10.7507/1001-5515.202312070 復制
版權信息： ?四川大學華西醫院華西期刊社《生物醫學工程學雜志》版權所有，未經授權不得轉載、改編
0 引言
心力衰竭（hearth failure，HF）（以下簡稱：心衰），是心臟結構或功能異常導致心室充盈或射血能力受損的一組復雜臨床綜合征。2012—2015年進行的中國高血壓調查研究顯示，我國35歲以上成人心衰患病率約為1.3%，涉及1 370萬人[1-2]。目前，基于循證醫學證據的主要心衰治療措施包括“新四聯”藥物治療和心臟再同步化治療等器械治療[3]。通過藥物及現有的器械治療措施，雖可改善近期血流動力學指標并減輕癥狀，但有相當比例終末期心衰患者對上述措施低反應[2]，因而需進一步接受心室輔助裝置植入[4]。現有的主流心室輔助裝置，通過機械泵連接左心室（left ventricle，LV）和主動脈血流來實現心臟泵功能和血液輸送及回流[5]。由于其直接接觸血液，必須長期服用抗凝血藥物，不可避免出現敗血癥、血栓、心衰加重等問題[6]，且手術創傷大，不利于康復。
直接心室輔助裝置（direct cardiac compression，DCC）可包裹住心臟并與心臟的跳動進行同頻柔性擠壓來輔助泵血，無需在心室及主動脈開孔，大大降低了手術難度及術后創傷[7-8]。雖然DCC已有40年的研究歷史，但由于心臟按壓的生物力學效應相關研究很少，其臨床應用一直受到限制[9]，如何以正確的方式將壓迫施加給心臟是一個值得討論的問題。
目前，已有的仿真模型大多以理想的正弦曲線力加載在心室壁上，且認為壓迫峰值與收縮末期重合[10-11]。然而在現實中，由于DCC結構的復雜性，要保持與心臟自然射血周期同頻工作是一件很困難的事情，施加壓迫力開始時刻與心臟開始收縮的時刻有不可避免的誤差。這種誤差可能會影響裝置的輔助效果，增加患者的負荷。為此，參考外科醫生施加壓迫的手法[12]，本文提出了在收縮初期開始施加壓迫，射血開始時達到壓迫力峰值，并在整個射血期間維持壓迫力峰值的壓迫方式。由于該方式維持了一段時間的峰值壓迫力，即使在DCC啟動時刻存在滯后的情況下，壓迫力峰值與心肌收縮力峰值也會重合，從而減小DCC輔助效果受到上述誤差的影響。
為了驗證該方式的合理性，本研究通過有限元方法構建人體LV的仿真模型，對比分析正弦加載和在射血階段維持峰值力的兩種加載模式的輔助效果，同時通過改變壓迫開始時間來模擬相位誤差，進一步對比兩種工作模式受誤差影響的結果。通過上述研究，本文期望能探究更優的DCC工作模式，以實現在盡量減小心肌的應力和應變的同時最大化提高輸出量。
1 材料與方法
本研究使用的心臟核磁共振成像數據來自心臟圖譜項目（Cardiac Atlas Project）中的桑尼布魯克心臟數據集（Sunnybrook cardiac data，SCD），該數據集對公眾提供開放訪問和數據下載[13]，其研究對象為一名42歲的心衰男性。
本文所描述的三維人體LV模型由以下部分組成：患者個性化LV網格模型、肌纖維結構、被動心肌本構、主動張力模型、體循環參數。求解器采用有限元分析軟件Abaqus 2018（SIMULIA Inc., 美國），本構模型通過有限元分析軟件Abaqus 2018（SIMULIA Inc., 美國）自帶的用戶子程序VUMAT實現。
1.1 左心室幾何模型及纖維結構的建立
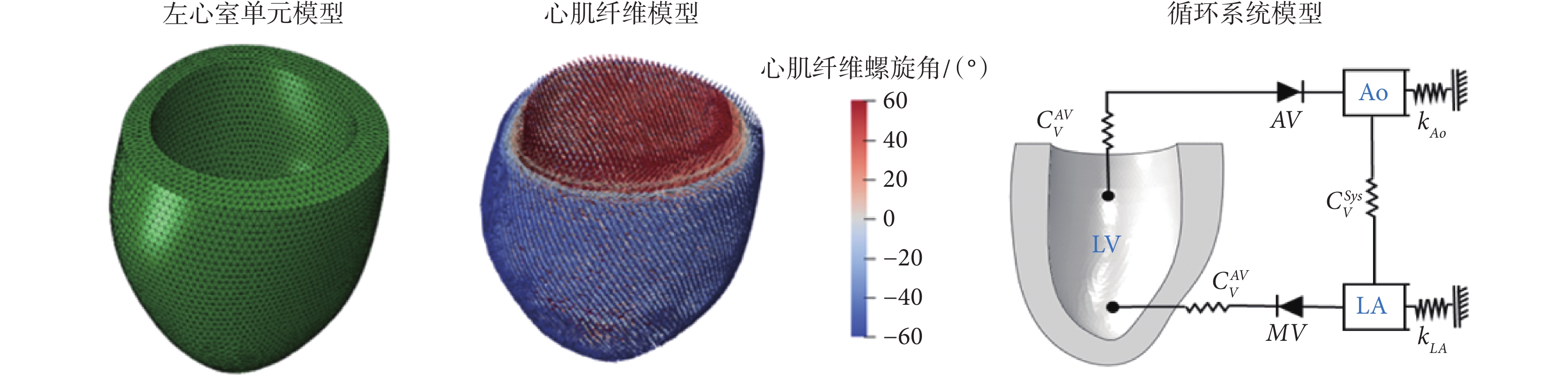
LV幾何模型選取舒張初期為初始構型，此時LV的體積和壓力都最小且最接近空載構型狀態。心衰LV的幾何模型基于核磁共振圖像由Guan等[14]的公開算法生成，如圖1所示，共72 956個四面體單元，16 268個節點。心肌纖維方向定義為從心外膜到心內膜呈線性變化。根據Streeter等[15]先前的實驗測量，LV的心內膜肌纖維螺旋角（αendo）、心外膜肌纖維螺旋角（αepi）規定為：αendo = 60°、αepi = ? 60°，結果如圖1所示。
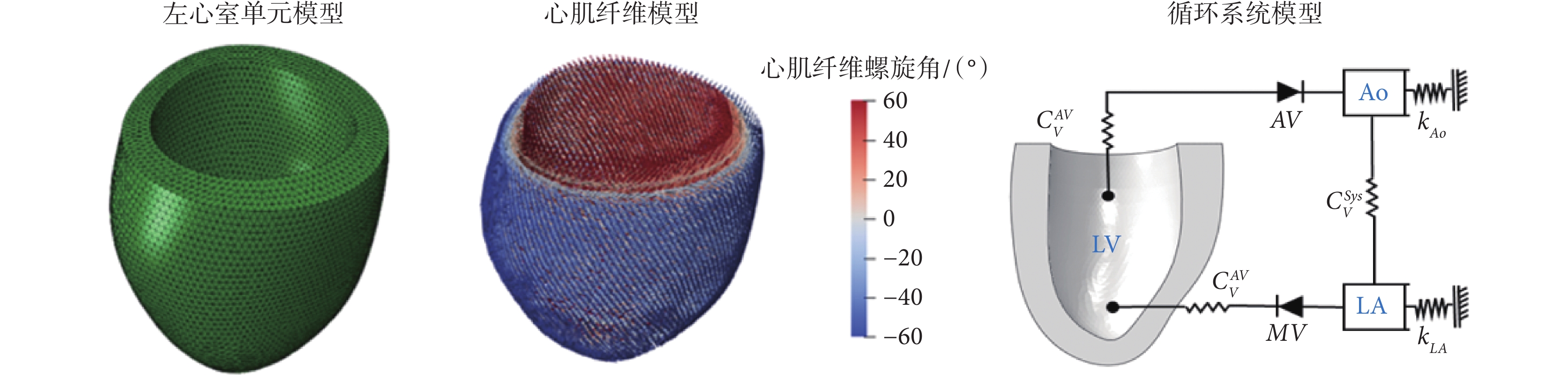圖1
LV有限元模型
Figure1.
LV finite element model
已有研究通過實驗證明，心肌纖維不會沿著平均纖維方向完全排列，而是離散分布的[16-17]。本文遵循纖維離散模型[18]，參考Guan等[14]的參數，心肌纖維在單位半球區域內的平均纖維方向呈正態分布。
1.2 心肌材料本構與參數
本文采用了Holzapfel等[19]提出的基于不變量的纖維增強本構模型，該模型考慮了心肌的形態和結構，將LV心肌的被動特性建模為非均勻的、厚壁的、不可壓縮的、正交各向異性的非線性彈性材料，具體參數如表1所示。心肌的主動應力如式(1)所示：
表1
被動本構模型參數
Table1.
Passive constitutive model parameters
 |
其中，Ta為沿纖維方向產生的主動張力，
，F為變形梯度，f0為平均心肌纖維方向，s0為平均片層纖維方向，n0為s0的法向向量，
，
，
，nf、ns、nn為主動張力在各自方向上的比例，參考Guan等[20]的參數，nf = 0.086，ns = 0.268，nn = 0.646，“?”代表張量積。
主動張力的時變彈性模型[21]，如式(2)所示：
 |
其中，Tmax是最大收縮力，代表心肌組織能夠產生的最大等距張力。Ca0為細胞內鈣離子濃度的峰值，ECa50為鈣敏感性，Ct為時間相關性函數，如式(3)～式(5)所示：
 |
 |
 |
其中，(Ca0)max是細胞內鈣濃度的最大峰值，B是一個常數，l為當前肌節長度，
。l0是主動張力時的肌節長度，t0是張力峰值的時間，tr是松弛的時間，
。m、b為支配松弛時間與肌節長度關系的常數，lr為無應力肌節長度。E是格林—拉格朗日應變張量，其中下角標f、s和n分別表示肌纖維、片層和片層法線方向。
心衰LV的被動心肌參數分別由Mangion等[22]的模型參數重新縮放，根據舒張末期容積（end-diastolic volume，EDV）確定，如表1所示。其中a、b、af、bf、as、bs、afs和bfs是與纖維方向有關的8個材料常數。另一方面，根據收縮末期容積（end-systolic volume，ESV）縮放主動收縮模型參數的Tmax，所得數值如表2所示。
表2
主動收縮模型參數
Table2.
Active shrink model parameters
1.3 循環系統模型
根據血流動力學與電學系統的等效規律[23]，將簡化閉環集總參數循環系統與LV模型耦合，包括主動脈腔（aorta，Ao）和左心房（left atrium，LA）腔。如圖1所示循環系統模型中，二尖瓣（mitral valve，MV）和主動脈瓣（aortic valve，AV）的功能通過單向流體交換來實現。CVAV、CVMV、CVSys分別代表AV、MV和體循環的阻抗，CVAV = 1.2、CVMV = 1.0、CVSys = 100，單位為MPa·mm2/t。kAo、kLA為兩個接地的彈簧，代表LV和Ao的順應性，kAo = 0.8、kLA = 1.0，單位為k/(N·mm)。通過有限元分析軟件Abaqus 2018（SIMULIA Inc.，美國）的流體腔和流體交換模塊實現了簡化的循環模型。該模型類似于彈性腔模型（windkessel models）[24]。
參考正常生理參數的研究，設置每個腔室的加載壓力作為本研究的初始條件，由于心衰患者的舒張末期壓力相比健康受試者通常高出10～25 mm Hg[25-26]，設置初始條件為LV腔：14 mm Hg、Ao：100 mm Hg、LA腔：14 mm Hg。整個過程如下：首先將模型LV預加載至正常LV舒張末期壓力，以達到舒張末期狀態，然后開始等容收縮，心室的壓力增加到超過Ao的壓力，AV打開，LV開始射血（t ≈ 0.1 s），整個心動周期為0.65 s。
1.4 不同模式的心外膜壓迫
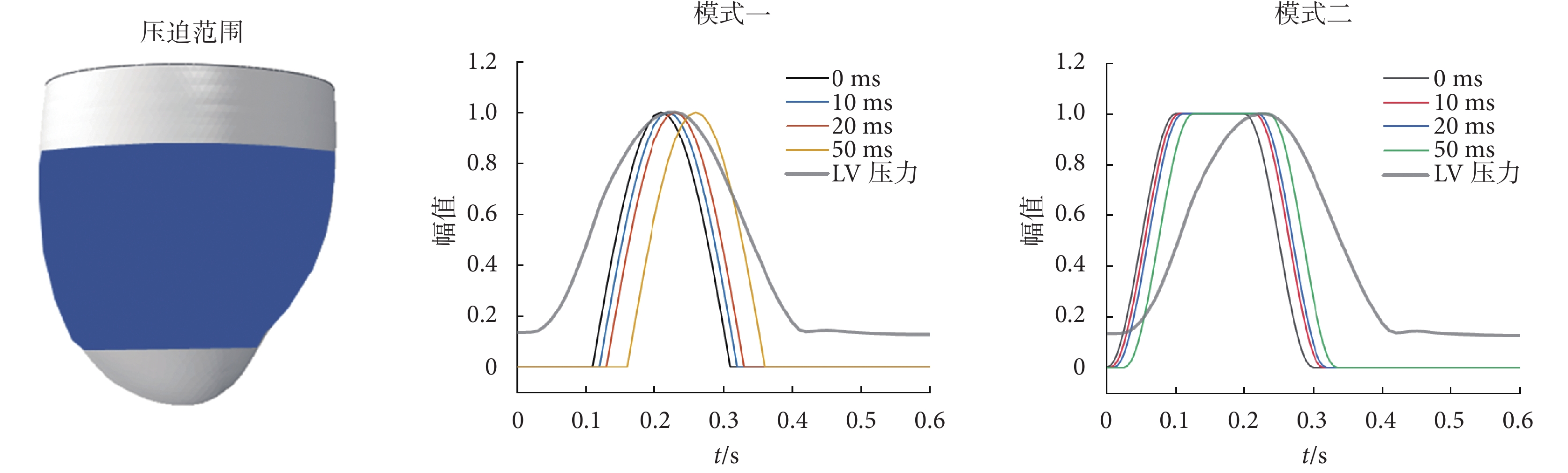
Aranda-Michel等[27]通過在理想橢球體LV上施加壓迫得出結論：對LV壓迫區域進行細分，對于血流動力學幾乎沒有影響。因此，本文選擇覆蓋LV中部大部分區域的壓迫范圍，覆蓋面積為11 278.63 mm2，如圖2所示。
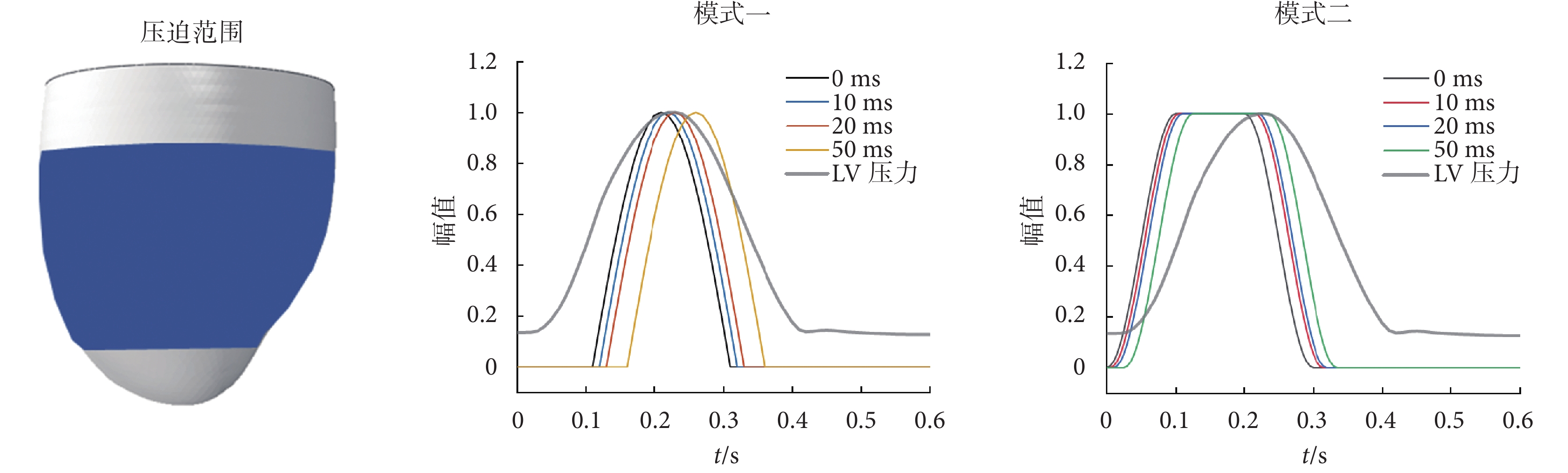圖2
壓迫模式示意圖
Figure2.
Compression mode diagram
傳統直接輔助壓迫的正弦曲線，開始于LV射血初始時刻，在射血結束時達到峰值，在等容舒張末期附近降為零[27]，本文將這種壓迫模式記作模式一；本文提出的另一種壓迫幅值曲線在心室收縮時壓迫力逐漸增加，直到開始射血時達到峰值，并在整個射血期間，受力均保持在峰值不變，之后逐漸降低為零，本文將該曲線記作模式二；兩種壓迫模式的曲線如圖2所示，計算公式如式(6)～式(7)所示：
 |
 |
其中，p(t)為壓迫力幅值；t=0為舒張末期時刻，心室開始收縮；0～0.1 s為等容收縮階段；0.1～0.2 s為快速射血期，之后心肌收縮力減小；0.2～0.3 s為減慢射血期，之后AV關閉，射血結束，0.65 s為一個心跳周期的總時長。
為了模擬DCC工作周期的誤差，參考第一心音時長約為100 ms，將模式一和模式二從最初的開始時間分別向后移動了10 ms、20 ms和50 ms（第一心音時長的50%），所有的模擬均運行4次循環，LV壓力與容積變化趨于穩定。
Obiajulu等[26]通過使用半球形DCC裝置的簡單模型來估計DCC裝置致動器的力需求，參考其施加的壓力范圍，施加峰值為5 kPa的負載（本模型LV最大血壓約為16 kPa）。
1.5 模型有效性驗證
如表3所示，本文對比了EDV、ESV和射血分數（ejection fractions，EF）的模擬值和核磁共振圖像的測量值，可以看出EDV、ESV和EF的模擬值和測量值誤差都在1%以內。
表3
模型結果對比
Table3.
Comparison of model results
另一方面，參考Kuijer等[28]根據短軸和長軸核磁共振圖像中標記點的位移，描述了整個人類LV三維位移和應變演變的正常范圍。將本文LV三個部位的應變結果與之進行對比，包括周向應變和軸向應變。這些應變計算均以舒張末期作為初始構型，選擇單個心動周期內收縮末期作為比較時間節點，所有應變均表示為格林—拉格朗日應變，如式（8）所示：
 |
 |
其中，ec、el分別是周向和縱向方向上的單位向量，由前文計算可得，C為右柯西—格林變形張量。因此，格林—拉格朗日應變定義如式(10)所示：
 |
對比結果如表4所示，表4中所有數據均表示為均值±標準差，可以看出，除了在心尖部的軸向應變外，其它所有應變都在臨床數據的兩個標準偏差范圍內，以上結果共同證明了模型的有效性。
表4
收縮末期應變對比（x ± s）
Table4.
Comparison of end-systolic strain（x ± s）
2 結果
2.1 兩種輔助模式效果對比
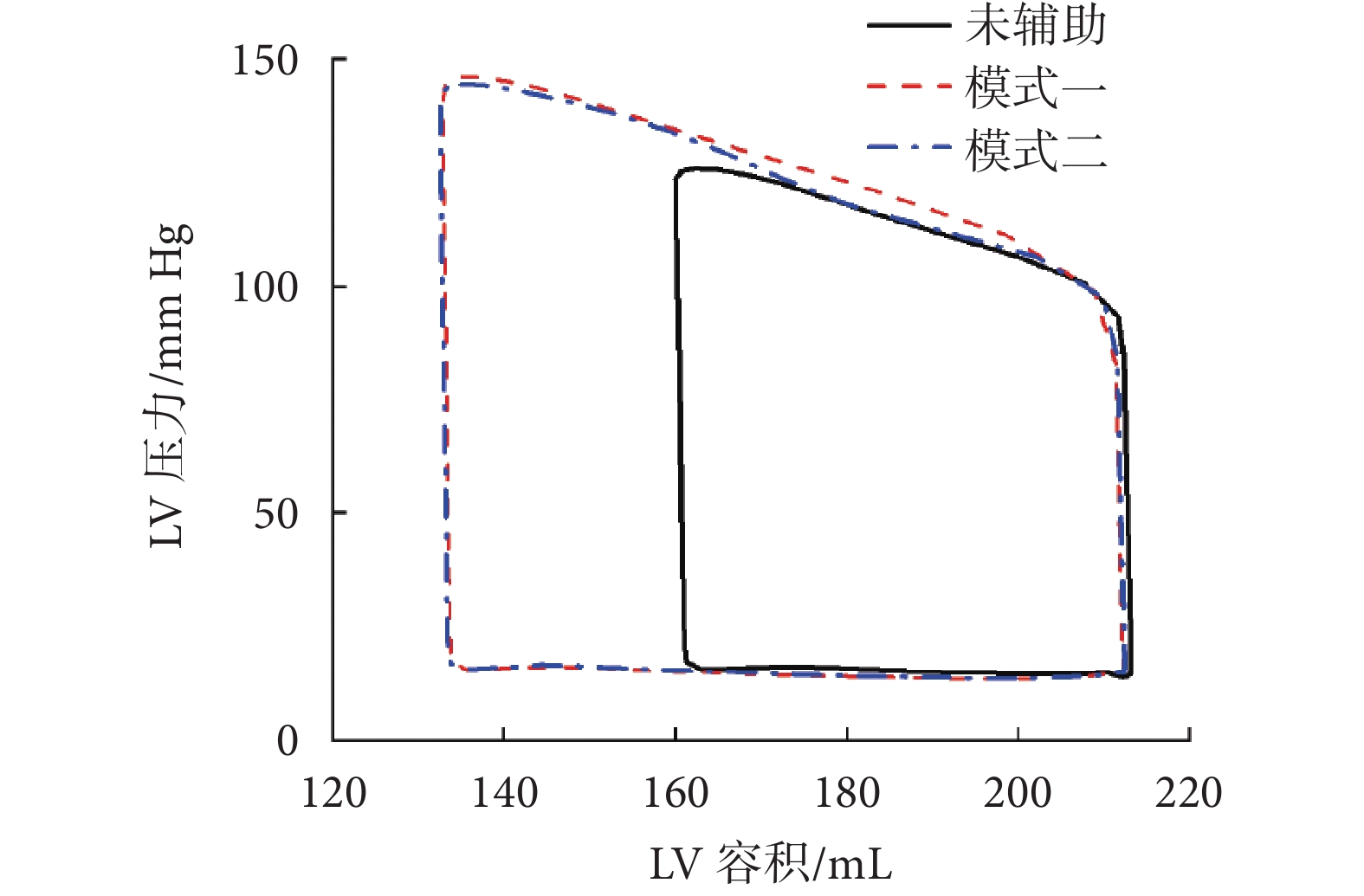
評價血流動力學的最佳方法是使用壓力—容積曲線，兩種壓迫模式與心衰LV的壓力—容積曲線如圖3所示。
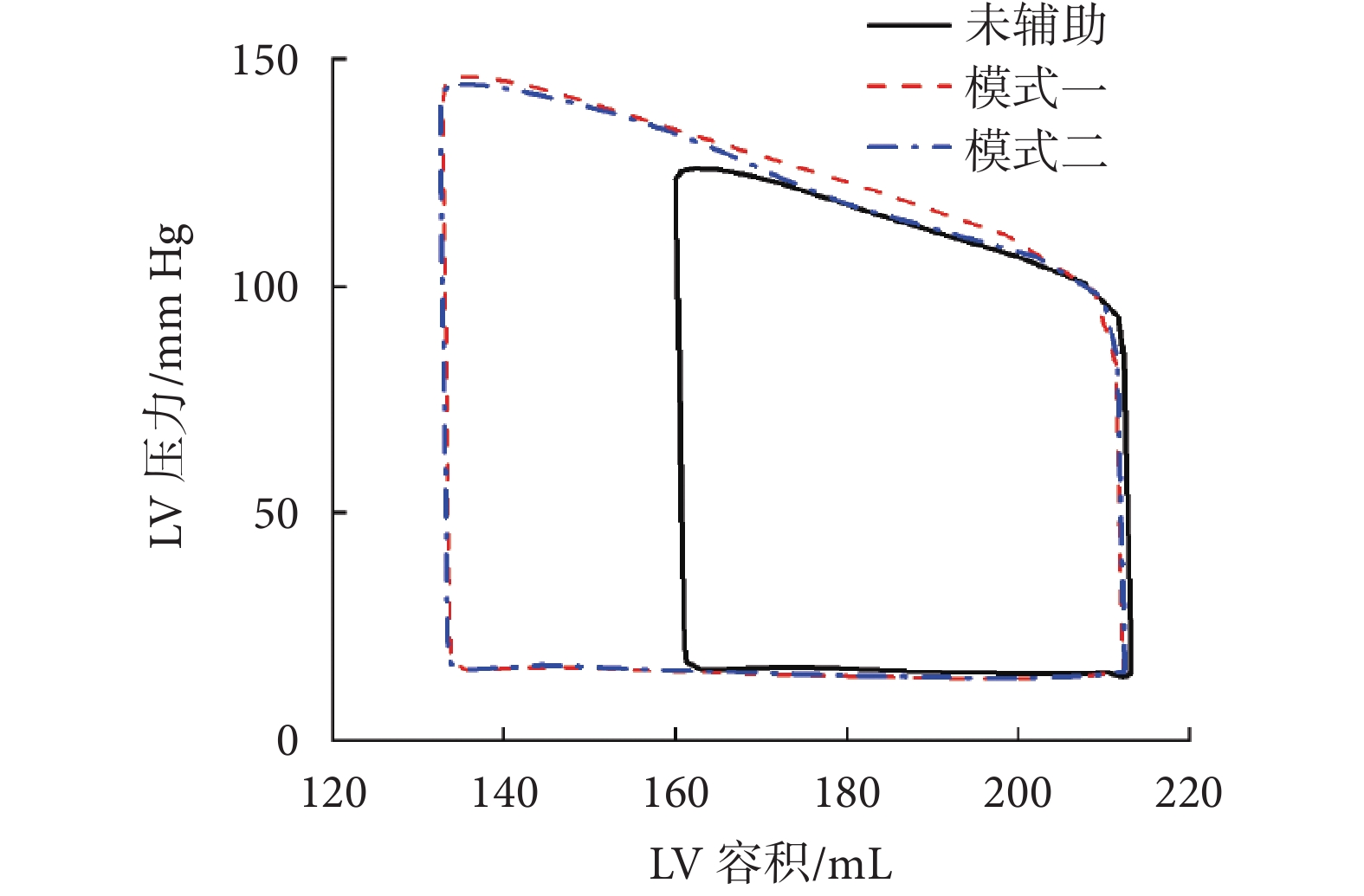圖3
壓力容積曲線
Figure3.
Pressure-volume loop
整體上可以看出，兩種模式壓迫下的壓力—容積曲線幾乎重疊，說明兩種模式的每搏輸出量（stroke volume，SV）、EF、峰值壓力（peak pressure，PP）和每搏功（stroke work，SW）對于未施加壓迫的LV都有所提升，且增加量近似相等，兩種壓迫模式下的LV血流動力學參數具體值如表5所示。
表5
血流動力學參數
Table5.
Hemodynamic parameters
在收縮末期時心肌收縮力達到最大，此時心肌纖維主應力（以σff表示）分布如圖4所示。施加壓迫之后，位于心尖部的應力集中有明顯改善，且整體的應力分布有所減小。
圖4
收縮末期LV心肌纖維應力分布
Figure4.
Fiber stress distribution in the LV end-systole
2.2 考慮相位誤差情況下兩種輔助模式效果的對比
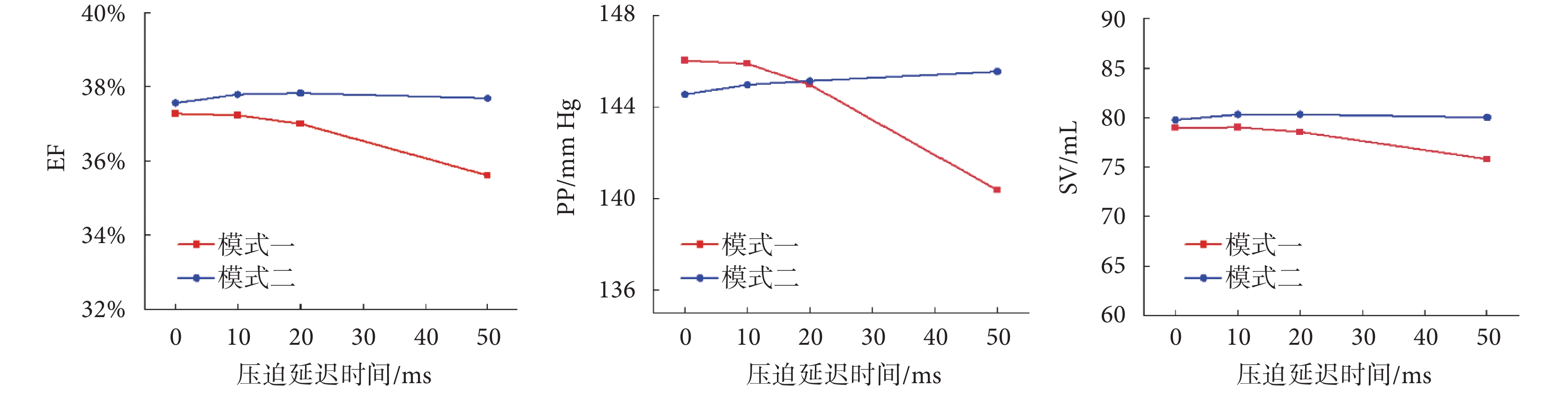
延遲兩種模式壓迫開始時間，血流動力學參數結果如圖5所示，包括EF、PP和SV。從中可以看出， 隨著壓迫開始延遲時間的增加，模式一的各項血流動力學參數都有所下降，當延遲時間增大到50 ms時，EF下降了2%，PP下降了6 mm Hg，SV下降了4 mL，而模式二的各項血流動力學參數都基本保持穩定。
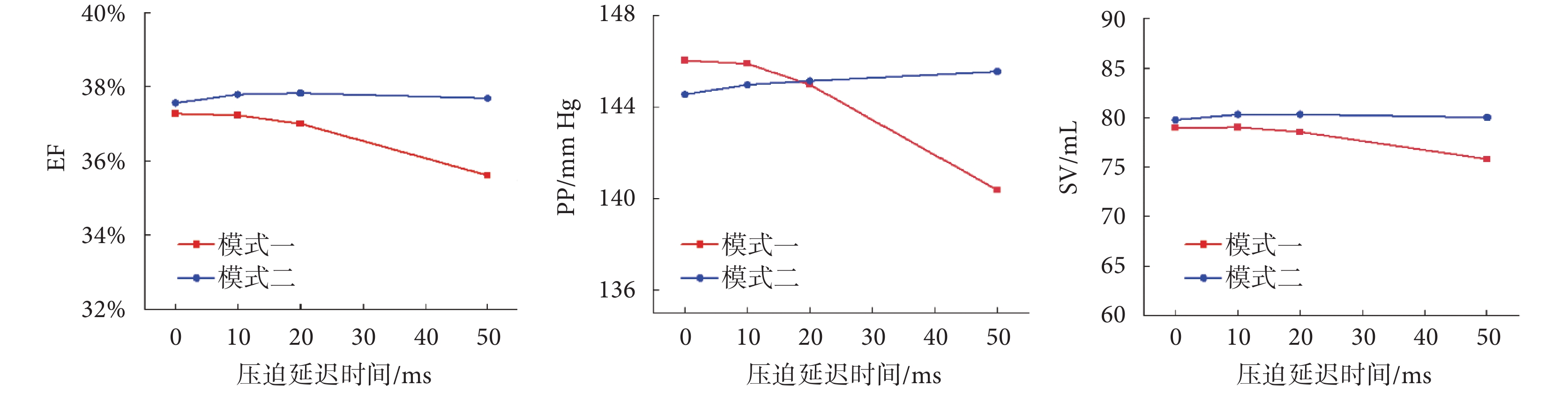圖5
血流動力學參數
Figure5.
Hemodynamic parameters
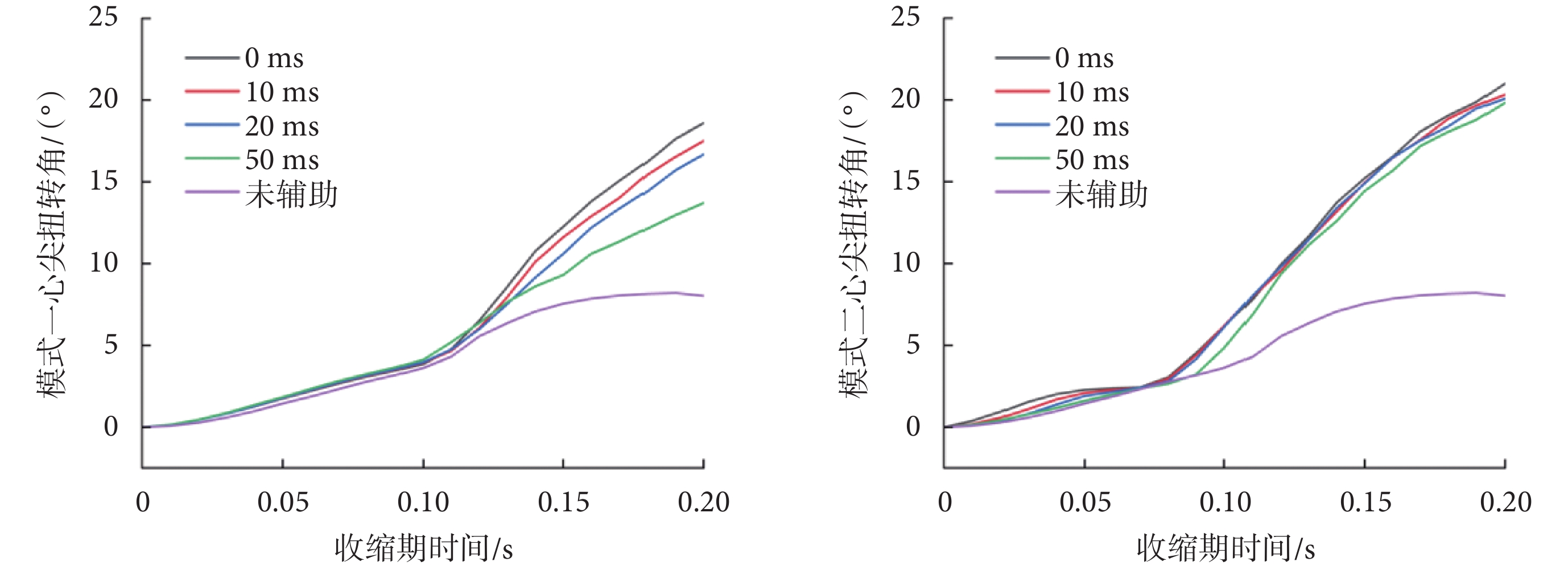
心尖扭轉角是LV尖部相對于基部旋轉的角度，在射血過程中，心內膜纖維間質變形產生勢能，隨后扭轉變形[29]。模式一和模式二在0.00～0.20 s之間收縮過程中的心尖扭轉角變化如圖6所示。可以看出，當壓迫開始時刻與射血開始時刻同步時，模式一在收縮末期的心尖扭轉角為18.6°，模式二在收縮末期的心尖扭轉角為20.3°，相差不大。隨著壓迫開始時間的滯后，模式一的心尖扭轉角逐漸減小，在50 ms時為13.7°；模式二的心尖扭轉角度依舊保持穩定。
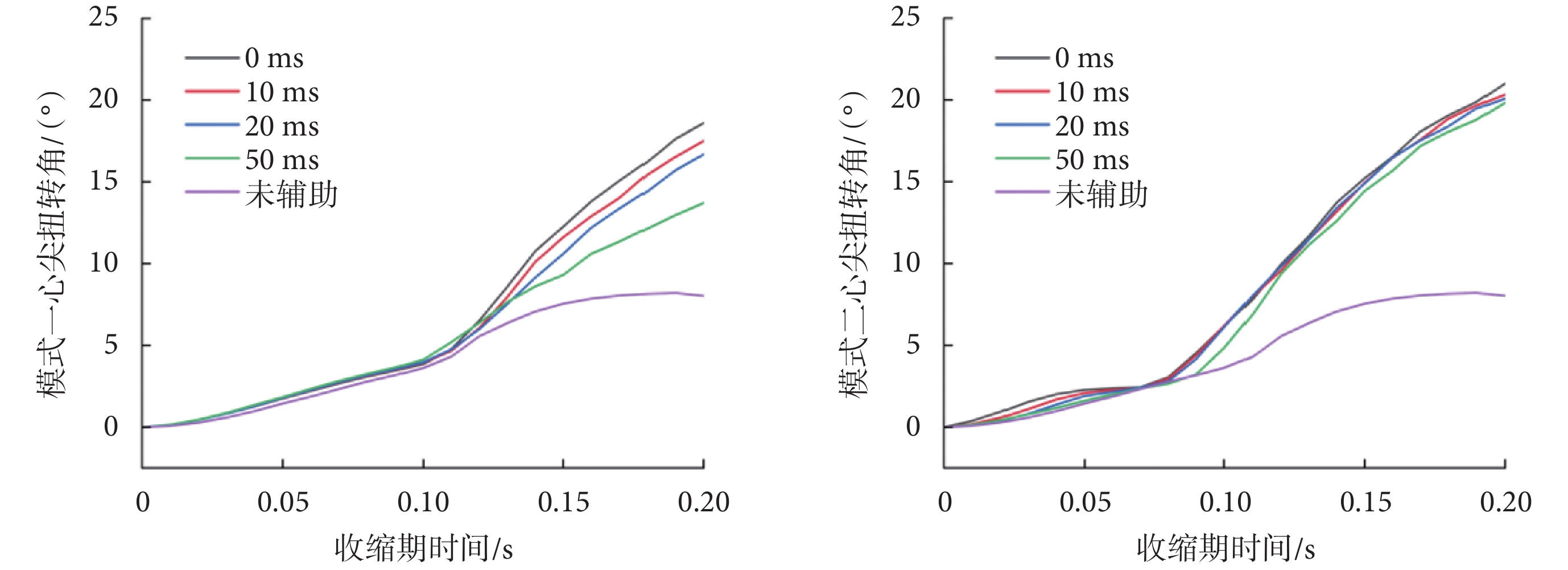圖6
心尖扭轉角
Figure6.
Heart apex twist angle
2.3 兩種輔助模式對左心室生物力學的影響
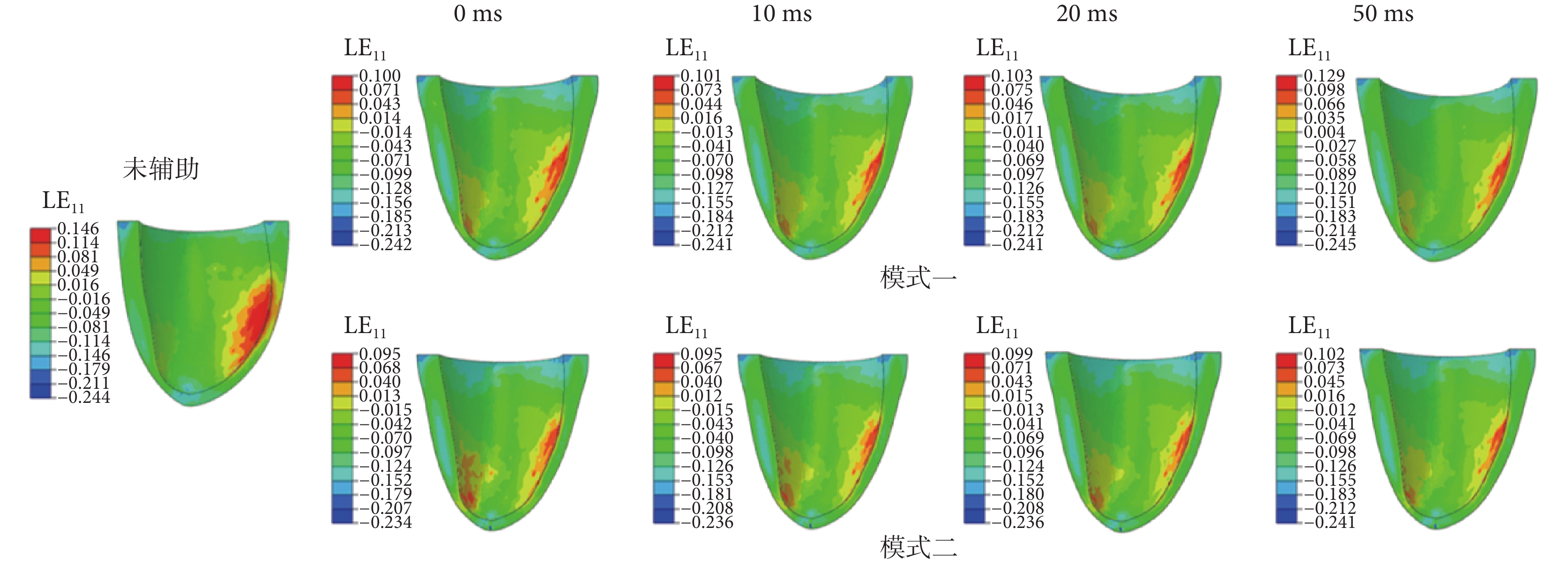
不同開始時間點的LV收縮末期相對于心跳周期開始時刻的纖維應變分布如圖7所示，圖7中數據均為真實應變（以LE11表示）。從圖7中可以看出，兩種模式的壓迫均可以減小LV收縮末期的最大纖維應變。未施加外膜輔助壓迫時，最大纖維應變為14.6%。當壓迫開始時間沒有延遲時，模式一和模式二的最大纖維應變分別為10.0%和9.5%，近似相等。隨著壓迫開始時間的滯后，兩種模式的心肌纖維應變均增大，但模式一增加的更多，當滯后時間為50 ms時，模式一的最大纖維應變為12.9%，模式二的最大纖維應變為10.2%。相對于模式一，改變壓迫開始時間對模式二的最大心肌纖維應變幾乎沒有影響。
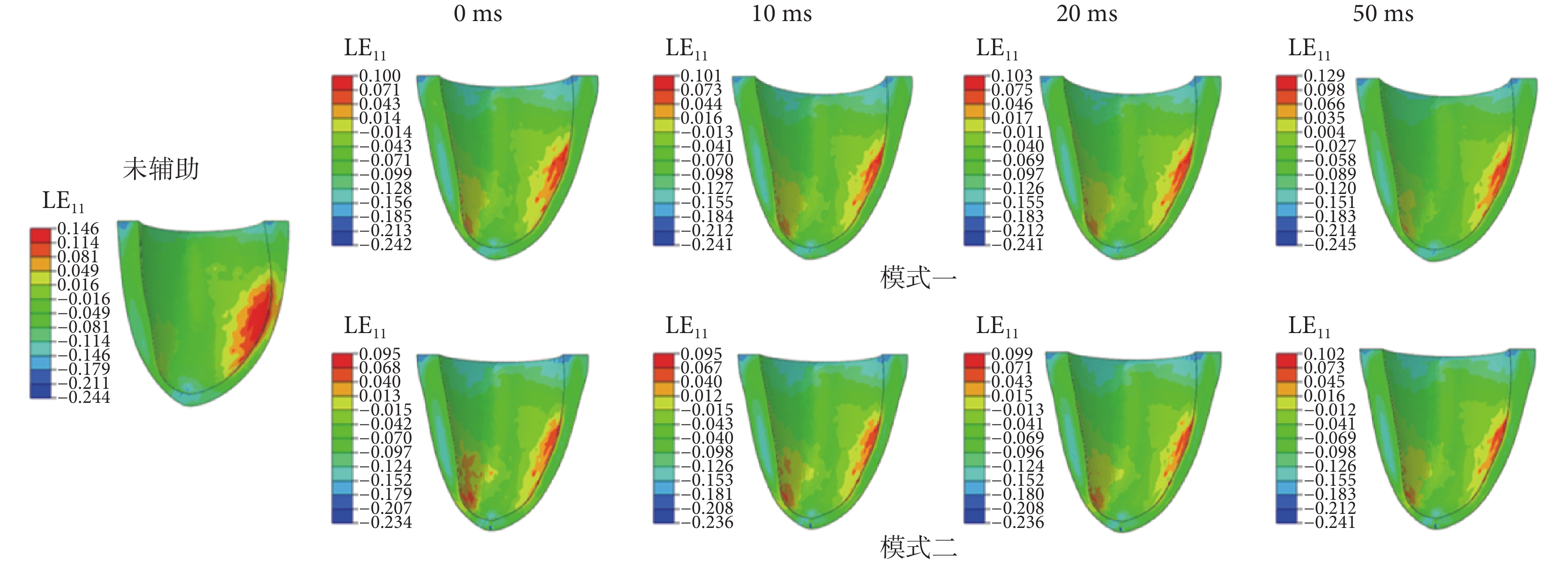圖7
不同壓迫開始時間的纖維應變分布
Figure7.
Fiber strain distribution at different compression start time
3 討論
本文針對心衰患者構建了個性化LV有限元模型，在此基礎上分別施加了正弦曲線及維持一段時間PP的心外膜輔助模式。
對比來看，在血流動力學參數方面，兩種輔助模式下的EF、PP和SV都有所上升，其中LV的EF分別從29.33 %提升到37.32 % 和37.77 %，可以維持患者的正常生理活動（EF降低型心衰的基線EF為40%）。
從生物力學的結果來看，兩種模式的壓迫都可以增加LV收縮能力及改善應力集中。收縮末期時LV處于收縮狀態，心肌纖維長度小于靜息長度，如圖7所示，最大心肌纖維應變減小說明LV的收縮能力增強。從圖4可以看出，由于心尖部心肌壁較薄，所以有明顯的應力集中現象，長時間的應力集中可能導致局部心肌梗死，施加心外膜輔助可以很大程度改善應力集中。
本文認為有兩個方面的原因導致了應力和應變的減小。第一，由于心肌纖維本身的結構特點，心肌纖維在心外膜處與周向成? 60°，在心內膜處為60°，心內壁區域下心肌纖維更接近于軸向方向，并且心肌纖維在沿著纖維方向上的硬度遠遠高于橫向方向。在心外膜施加壓迫時，心室被拉長，纖維有向心尖處伸展的趨勢，處于收縮狀態的心肌沿纖維方向的加載減小，因此心肌纖維的應力和應變都減小。第二，施加心外膜輔助可增強LV的扭轉能力。如圖6所示，施加模式一和模式二的壓迫后，收縮末期心尖扭轉角從8.0°增加到了18.6°和20.3°，恢復正常扭轉能力，該數據參考Badano等[29]測量的健康人收縮末期心尖扭轉角約為16°。當纖維達到收縮峰值時，沿纖維方向的應力會很大，且心內膜收縮力大于心外膜，但由于心外膜半徑較大，心外膜處可以產生更大的扭矩以控制旋轉方向。在射血期間，心外膜下心肌較大的扭矩經壁耦合至心肌中層和心內膜下心肌，導致LV整體旋轉。在心外膜下，這種扭矩有助于主纖維方向的收縮；在中層，扭轉動作增強了圓周方向的縮短；在心內膜下，扭轉動作可引起肌纖維重新排列，使得心內膜下肌纖維沿纖維的法向方向更緊密地排列以增厚左室壁。扭轉減小會增加心內膜應力和應變，從而增加需氧量，降低LV收縮功能的效率[29]，提高心室的扭轉角有助于使纖維應力和肌纖維的縮短沿室壁均勻分布。
進一步推遲壓迫開始時間以模擬相位誤差的影響，根據血流動力學結果顯示，壓迫開始時間的滯后會削弱模式一輔助效果，EF、SV和PP都有所下降。具體而言，EF在壓迫延遲50 ms時從37.32%下降到35.60%，相對于理想情況下的EF提升，效果降低。從圖5可以看出，模式二的各項血流動力學結果基本保持穩定不受影響。這是由于模式二在整個射血期間都維持了壓迫力峰值，盡管壓迫開始時間滯后，在收縮末期時心外膜壓迫力仍與心肌纖維收縮力同時處于峰值，因此對誤差的抵抗能力較強。從生物力學角度來看，模式一的心尖扭轉能力下降，在壓迫延遲50 ms時從18.6°下降到13.7°，模式二基本維持在20.0°左右。模式一的心尖扭轉能力減弱，心室收縮效率也降低，心肌纖維需要更大的變形來實現收縮動作，如圖7所示，模式一的心肌的纖維最大應變從10.0%增大到12.9%，模式二的心肌纖維最大應變依舊保持不變，說明本文提出的加載模式在減小心肌應變方面能力更強，從而在引導心衰心肌的反向良性重塑方面更有優勢。
本文的研究也存在一定的局限性：首先，本文僅考慮了LV的模型，而未對其他心腔的運動情況進行模擬。其次，所建立的簡化體外循環系統耦合并不能完全模擬人體的血液循環系統。在下一步工作中，將考慮多個心腔的交互，搭建更為復雜的系統，同時根據不同程度的心衰情況建立不同類型的心臟模型，以進一步比較不同的心外膜輔助方式對心臟生物力學的影響，旨在為DCC的設計與優化、臨床治療和術后康復提供理論支持。
4 結論
本文所提出的維持一段時間峰值壓迫力的模式和傳統正弦加載壓迫力模式相比，帶來的血流動力學參數提升近似相等，并且心肌的生物力學結果也近似相同。然而，由于DCC工作周期和心臟跳動周期存在的相位誤差，正弦加載壓迫力模式的血流動力學參數有所下降，心室的收縮能力也有所降低。相比之下，本文所提出的維持峰值壓迫力的模式，可以在誤差為50 ms的情況下保持血流動力學參數及心肌纖維應力、應變不受影響，因此可對DCC設計和優化提供理論指導。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：李宸、徐俊波和張小剛構思方案，李宸實施方案并處理數據，張盛負責作圖，強賢杰、王天博、劉曉翰、張悅、黃剛、徐俊波和靳忠民討論并修改了論文。
0 引言
心力衰竭（hearth failure，HF）（以下簡稱：心衰），是心臟結構或功能異常導致心室充盈或射血能力受損的一組復雜臨床綜合征。2012—2015年進行的中國高血壓調查研究顯示，我國35歲以上成人心衰患病率約為1.3%，涉及1 370萬人[1-2]。目前，基于循證醫學證據的主要心衰治療措施包括“新四聯”藥物治療和心臟再同步化治療等器械治療[3]。通過藥物及現有的器械治療措施，雖可改善近期血流動力學指標并減輕癥狀，但有相當比例終末期心衰患者對上述措施低反應[2]，因而需進一步接受心室輔助裝置植入[4]。現有的主流心室輔助裝置，通過機械泵連接左心室（left ventricle，LV）和主動脈血流來實現心臟泵功能和血液輸送及回流[5]。由于其直接接觸血液，必須長期服用抗凝血藥物，不可避免出現敗血癥、血栓、心衰加重等問題[6]，且手術創傷大，不利于康復。
直接心室輔助裝置（direct cardiac compression，DCC）可包裹住心臟并與心臟的跳動進行同頻柔性擠壓來輔助泵血，無需在心室及主動脈開孔，大大降低了手術難度及術后創傷[7-8]。雖然DCC已有40年的研究歷史，但由于心臟按壓的生物力學效應相關研究很少，其臨床應用一直受到限制[9]，如何以正確的方式將壓迫施加給心臟是一個值得討論的問題。
目前，已有的仿真模型大多以理想的正弦曲線力加載在心室壁上，且認為壓迫峰值與收縮末期重合[10-11]。然而在現實中，由于DCC結構的復雜性，要保持與心臟自然射血周期同頻工作是一件很困難的事情，施加壓迫力開始時刻與心臟開始收縮的時刻有不可避免的誤差。這種誤差可能會影響裝置的輔助效果，增加患者的負荷。為此，參考外科醫生施加壓迫的手法[12]，本文提出了在收縮初期開始施加壓迫，射血開始時達到壓迫力峰值，并在整個射血期間維持壓迫力峰值的壓迫方式。由于該方式維持了一段時間的峰值壓迫力，即使在DCC啟動時刻存在滯后的情況下，壓迫力峰值與心肌收縮力峰值也會重合，從而減小DCC輔助效果受到上述誤差的影響。
為了驗證該方式的合理性，本研究通過有限元方法構建人體LV的仿真模型，對比分析正弦加載和在射血階段維持峰值力的兩種加載模式的輔助效果，同時通過改變壓迫開始時間來模擬相位誤差，進一步對比兩種工作模式受誤差影響的結果。通過上述研究，本文期望能探究更優的DCC工作模式，以實現在盡量減小心肌的應力和應變的同時最大化提高輸出量。
1 材料與方法
本研究使用的心臟核磁共振成像數據來自心臟圖譜項目（Cardiac Atlas Project）中的桑尼布魯克心臟數據集（Sunnybrook cardiac data，SCD），該數據集對公眾提供開放訪問和數據下載[13]，其研究對象為一名42歲的心衰男性。
本文所描述的三維人體LV模型由以下部分組成：患者個性化LV網格模型、肌纖維結構、被動心肌本構、主動張力模型、體循環參數。求解器采用有限元分析軟件Abaqus 2018（SIMULIA Inc., 美國），本構模型通過有限元分析軟件Abaqus 2018（SIMULIA Inc., 美國）自帶的用戶子程序VUMAT實現。
1.1 左心室幾何模型及纖維結構的建立
LV幾何模型選取舒張初期為初始構型，此時LV的體積和壓力都最小且最接近空載構型狀態。心衰LV的幾何模型基于核磁共振圖像由Guan等[14]的公開算法生成，如圖1所示，共72 956個四面體單元，16 268個節點。心肌纖維方向定義為從心外膜到心內膜呈線性變化。根據Streeter等[15]先前的實驗測量，LV的心內膜肌纖維螺旋角（αendo）、心外膜肌纖維螺旋角（αepi）規定為：αendo = 60°、αepi = ? 60°，結果如圖1所示。
圖1
LV有限元模型
Figure1.
LV finite element model
已有研究通過實驗證明，心肌纖維不會沿著平均纖維方向完全排列，而是離散分布的[16-17]。本文遵循纖維離散模型[18]，參考Guan等[14]的參數，心肌纖維在單位半球區域內的平均纖維方向呈正態分布。
1.2 心肌材料本構與參數
本文采用了Holzapfel等[19]提出的基于不變量的纖維增強本構模型，該模型考慮了心肌的形態和結構，將LV心肌的被動特性建模為非均勻的、厚壁的、不可壓縮的、正交各向異性的非線性彈性材料，具體參數如表1所示。心肌的主動應力如式(1)所示：
表1
被動本構模型參數
Table1.
Passive constitutive model parameters
|
其中，Ta為沿纖維方向產生的主動張力，，F為變形梯度，f0為平均心肌纖維方向，s0為平均片層纖維方向，n0為s0的法向向量，，，，nf、ns、nn為主動張力在各自方向上的比例，參考Guan等[20]的參數，nf = 0.086，ns = 0.268，nn = 0.646，“?”代表張量積。
主動張力的時變彈性模型[21]，如式(2)所示：
|
其中，Tmax是最大收縮力，代表心肌組織能夠產生的最大等距張力。Ca0為細胞內鈣離子濃度的峰值，ECa50為鈣敏感性，Ct為時間相關性函數，如式(3)～式(5)所示：
|
|
|
其中，(Ca0)max是細胞內鈣濃度的最大峰值，B是一個常數，l為當前肌節長度，。l0是主動張力時的肌節長度，t0是張力峰值的時間，tr是松弛的時間，。m、b為支配松弛時間與肌節長度關系的常數，lr為無應力肌節長度。E是格林—拉格朗日應變張量，其中下角標f、s和n分別表示肌纖維、片層和片層法線方向。
心衰LV的被動心肌參數分別由Mangion等[22]的模型參數重新縮放，根據舒張末期容積（end-diastolic volume，EDV）確定，如表1所示。其中a、b、af、bf、as、bs、afs和bfs是與纖維方向有關的8個材料常數。另一方面，根據收縮末期容積（end-systolic volume，ESV）縮放主動收縮模型參數的Tmax，所得數值如表2所示。
表2
主動收縮模型參數
Table2.
Active shrink model parameters
1.3 循環系統模型
根據血流動力學與電學系統的等效規律[23]，將簡化閉環集總參數循環系統與LV模型耦合，包括主動脈腔（aorta，Ao）和左心房（left atrium，LA）腔。如圖1所示循環系統模型中，二尖瓣（mitral valve，MV）和主動脈瓣（aortic valve，AV）的功能通過單向流體交換來實現。CVAV、CVMV、CVSys分別代表AV、MV和體循環的阻抗，CVAV = 1.2、CVMV = 1.0、CVSys = 100，單位為MPa·mm2/t。kAo、kLA為兩個接地的彈簧，代表LV和Ao的順應性，kAo = 0.8、kLA = 1.0，單位為k/(N·mm)。通過有限元分析軟件Abaqus 2018（SIMULIA Inc.，美國）的流體腔和流體交換模塊實現了簡化的循環模型。該模型類似于彈性腔模型（windkessel models）[24]。
參考正常生理參數的研究，設置每個腔室的加載壓力作為本研究的初始條件，由于心衰患者的舒張末期壓力相比健康受試者通常高出10～25 mm Hg[25-26]，設置初始條件為LV腔：14 mm Hg、Ao：100 mm Hg、LA腔：14 mm Hg。整個過程如下：首先將模型LV預加載至正常LV舒張末期壓力，以達到舒張末期狀態，然后開始等容收縮，心室的壓力增加到超過Ao的壓力，AV打開，LV開始射血（t ≈ 0.1 s），整個心動周期為0.65 s。
1.4 不同模式的心外膜壓迫
Aranda-Michel等[27]通過在理想橢球體LV上施加壓迫得出結論：對LV壓迫區域進行細分，對于血流動力學幾乎沒有影響。因此，本文選擇覆蓋LV中部大部分區域的壓迫范圍，覆蓋面積為11 278.63 mm2，如圖2所示。
圖2
壓迫模式示意圖
Figure2.
Compression mode diagram
傳統直接輔助壓迫的正弦曲線，開始于LV射血初始時刻，在射血結束時達到峰值，在等容舒張末期附近降為零[27]，本文將這種壓迫模式記作模式一；本文提出的另一種壓迫幅值曲線在心室收縮時壓迫力逐漸增加，直到開始射血時達到峰值，并在整個射血期間，受力均保持在峰值不變，之后逐漸降低為零，本文將該曲線記作模式二；兩種壓迫模式的曲線如圖2所示，計算公式如式(6)～式(7)所示：
|
|
其中，p(t)為壓迫力幅值；t=0為舒張末期時刻，心室開始收縮；0～0.1 s為等容收縮階段；0.1～0.2 s為快速射血期，之后心肌收縮力減小；0.2～0.3 s為減慢射血期，之后AV關閉，射血結束，0.65 s為一個心跳周期的總時長。
為了模擬DCC工作周期的誤差，參考第一心音時長約為100 ms，將模式一和模式二從最初的開始時間分別向后移動了10 ms、20 ms和50 ms（第一心音時長的50%），所有的模擬均運行4次循環，LV壓力與容積變化趨于穩定。
Obiajulu等[26]通過使用半球形DCC裝置的簡單模型來估計DCC裝置致動器的力需求，參考其施加的壓力范圍，施加峰值為5 kPa的負載（本模型LV最大血壓約為16 kPa）。
1.5 模型有效性驗證
如表3所示，本文對比了EDV、ESV和射血分數（ejection fractions，EF）的模擬值和核磁共振圖像的測量值，可以看出EDV、ESV和EF的模擬值和測量值誤差都在1%以內。
表3
模型結果對比
Table3.
Comparison of model results
另一方面，參考Kuijer等[28]根據短軸和長軸核磁共振圖像中標記點的位移，描述了整個人類LV三維位移和應變演變的正常范圍。將本文LV三個部位的應變結果與之進行對比，包括周向應變和軸向應變。這些應變計算均以舒張末期作為初始構型，選擇單個心動周期內收縮末期作為比較時間節點，所有應變均表示為格林—拉格朗日應變，如式（8）所示：
|
|
其中，ec、el分別是周向和縱向方向上的單位向量，由前文計算可得，C為右柯西—格林變形張量。因此，格林—拉格朗日應變定義如式(10)所示：
|
對比結果如表4所示，表4中所有數據均表示為均值±標準差，可以看出，除了在心尖部的軸向應變外，其它所有應變都在臨床數據的兩個標準偏差范圍內，以上結果共同證明了模型的有效性。
表4
收縮末期應變對比（x ± s）
Table4.
Comparison of end-systolic strain（x ± s）
2 結果
2.1 兩種輔助模式效果對比
評價血流動力學的最佳方法是使用壓力—容積曲線，兩種壓迫模式與心衰LV的壓力—容積曲線如圖3所示。
圖3
壓力容積曲線
Figure3.
Pressure-volume loop
整體上可以看出，兩種模式壓迫下的壓力—容積曲線幾乎重疊，說明兩種模式的每搏輸出量（stroke volume，SV）、EF、峰值壓力（peak pressure，PP）和每搏功（stroke work，SW）對于未施加壓迫的LV都有所提升，且增加量近似相等，兩種壓迫模式下的LV血流動力學參數具體值如表5所示。
表5
血流動力學參數
Table5.
Hemodynamic parameters
在收縮末期時心肌收縮力達到最大，此時心肌纖維主應力（以σff表示）分布如圖4所示。施加壓迫之后，位于心尖部的應力集中有明顯改善，且整體的應力分布有所減小。
圖4
收縮末期LV心肌纖維應力分布
Figure4.
Fiber stress distribution in the LV end-systole
2.2 考慮相位誤差情況下兩種輔助模式效果的對比
延遲兩種模式壓迫開始時間，血流動力學參數結果如圖5所示，包括EF、PP和SV。從中可以看出， 隨著壓迫開始延遲時間的增加，模式一的各項血流動力學參數都有所下降，當延遲時間增大到50 ms時，EF下降了2%，PP下降了6 mm Hg，SV下降了4 mL，而模式二的各項血流動力學參數都基本保持穩定。
圖5
血流動力學參數
Figure5.
Hemodynamic parameters
心尖扭轉角是LV尖部相對于基部旋轉的角度，在射血過程中，心內膜纖維間質變形產生勢能，隨后扭轉變形[29]。模式一和模式二在0.00～0.20 s之間收縮過程中的心尖扭轉角變化如圖6所示。可以看出，當壓迫開始時刻與射血開始時刻同步時，模式一在收縮末期的心尖扭轉角為18.6°，模式二在收縮末期的心尖扭轉角為20.3°，相差不大。隨著壓迫開始時間的滯后，模式一的心尖扭轉角逐漸減小，在50 ms時為13.7°；模式二的心尖扭轉角度依舊保持穩定。
圖6
心尖扭轉角
Figure6.
Heart apex twist angle
2.3 兩種輔助模式對左心室生物力學的影響
不同開始時間點的LV收縮末期相對于心跳周期開始時刻的纖維應變分布如圖7所示，圖7中數據均為真實應變（以LE11表示）。從圖7中可以看出，兩種模式的壓迫均可以減小LV收縮末期的最大纖維應變。未施加外膜輔助壓迫時，最大纖維應變為14.6%。當壓迫開始時間沒有延遲時，模式一和模式二的最大纖維應變分別為10.0%和9.5%，近似相等。隨著壓迫開始時間的滯后，兩種模式的心肌纖維應變均增大，但模式一增加的更多，當滯后時間為50 ms時，模式一的最大纖維應變為12.9%，模式二的最大纖維應變為10.2%。相對于模式一，改變壓迫開始時間對模式二的最大心肌纖維應變幾乎沒有影響。
圖7
不同壓迫開始時間的纖維應變分布
Figure7.
Fiber strain distribution at different compression start time
3 討論
本文針對心衰患者構建了個性化LV有限元模型，在此基礎上分別施加了正弦曲線及維持一段時間PP的心外膜輔助模式。
對比來看，在血流動力學參數方面，兩種輔助模式下的EF、PP和SV都有所上升，其中LV的EF分別從29.33 %提升到37.32 % 和37.77 %，可以維持患者的正常生理活動（EF降低型心衰的基線EF為40%）。
從生物力學的結果來看，兩種模式的壓迫都可以增加LV收縮能力及改善應力集中。收縮末期時LV處于收縮狀態，心肌纖維長度小于靜息長度，如圖7所示，最大心肌纖維應變減小說明LV的收縮能力增強。從圖4可以看出，由于心尖部心肌壁較薄，所以有明顯的應力集中現象，長時間的應力集中可能導致局部心肌梗死，施加心外膜輔助可以很大程度改善應力集中。
本文認為有兩個方面的原因導致了應力和應變的減小。第一，由于心肌纖維本身的結構特點，心肌纖維在心外膜處與周向成? 60°，在心內膜處為60°，心內壁區域下心肌纖維更接近于軸向方向，并且心肌纖維在沿著纖維方向上的硬度遠遠高于橫向方向。在心外膜施加壓迫時，心室被拉長，纖維有向心尖處伸展的趨勢，處于收縮狀態的心肌沿纖維方向的加載減小，因此心肌纖維的應力和應變都減小。第二，施加心外膜輔助可增強LV的扭轉能力。如圖6所示，施加模式一和模式二的壓迫后，收縮末期心尖扭轉角從8.0°增加到了18.6°和20.3°，恢復正常扭轉能力，該數據參考Badano等[29]測量的健康人收縮末期心尖扭轉角約為16°。當纖維達到收縮峰值時，沿纖維方向的應力會很大，且心內膜收縮力大于心外膜，但由于心外膜半徑較大，心外膜處可以產生更大的扭矩以控制旋轉方向。在射血期間，心外膜下心肌較大的扭矩經壁耦合至心肌中層和心內膜下心肌，導致LV整體旋轉。在心外膜下，這種扭矩有助于主纖維方向的收縮；在中層，扭轉動作增強了圓周方向的縮短；在心內膜下，扭轉動作可引起肌纖維重新排列，使得心內膜下肌纖維沿纖維的法向方向更緊密地排列以增厚左室壁。扭轉減小會增加心內膜應力和應變，從而增加需氧量，降低LV收縮功能的效率[29]，提高心室的扭轉角有助于使纖維應力和肌纖維的縮短沿室壁均勻分布。
進一步推遲壓迫開始時間以模擬相位誤差的影響，根據血流動力學結果顯示，壓迫開始時間的滯后會削弱模式一輔助效果，EF、SV和PP都有所下降。具體而言，EF在壓迫延遲50 ms時從37.32%下降到35.60%，相對于理想情況下的EF提升，效果降低。從圖5可以看出，模式二的各項血流動力學結果基本保持穩定不受影響。這是由于模式二在整個射血期間都維持了壓迫力峰值，盡管壓迫開始時間滯后，在收縮末期時心外膜壓迫力仍與心肌纖維收縮力同時處于峰值，因此對誤差的抵抗能力較強。從生物力學角度來看，模式一的心尖扭轉能力下降，在壓迫延遲50 ms時從18.6°下降到13.7°，模式二基本維持在20.0°左右。模式一的心尖扭轉能力減弱，心室收縮效率也降低，心肌纖維需要更大的變形來實現收縮動作，如圖7所示，模式一的心肌的纖維最大應變從10.0%增大到12.9%，模式二的心肌纖維最大應變依舊保持不變，說明本文提出的加載模式在減小心肌應變方面能力更強，從而在引導心衰心肌的反向良性重塑方面更有優勢。
本文的研究也存在一定的局限性：首先，本文僅考慮了LV的模型，而未對其他心腔的運動情況進行模擬。其次，所建立的簡化體外循環系統耦合并不能完全模擬人體的血液循環系統。在下一步工作中，將考慮多個心腔的交互，搭建更為復雜的系統，同時根據不同程度的心衰情況建立不同類型的心臟模型，以進一步比較不同的心外膜輔助方式對心臟生物力學的影響，旨在為DCC的設計與優化、臨床治療和術后康復提供理論支持。
4 結論
本文所提出的維持一段時間峰值壓迫力的模式和傳統正弦加載壓迫力模式相比，帶來的血流動力學參數提升近似相等，并且心肌的生物力學結果也近似相同。然而，由于DCC工作周期和心臟跳動周期存在的相位誤差，正弦加載壓迫力模式的血流動力學參數有所下降，心室的收縮能力也有所降低。相比之下，本文所提出的維持峰值壓迫力的模式，可以在誤差為50 ms的情況下保持血流動力學參數及心肌纖維應力、應變不受影響，因此可對DCC設計和優化提供理論指導。
重要聲明
利益沖突聲明：本文全體作者均聲明不存在利益沖突。
作者貢獻聲明：李宸、徐俊波和張小剛構思方案，李宸實施方案并處理數據，張盛負責作圖，強賢杰、王天博、劉曉翰、張悅、黃剛、徐俊波和靳忠民討論并修改了論文。
